
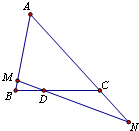
 在△ABC中,点D在线段BC上,且满足BD=$\frac{1}{2}$DC,过点D的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AM}$=m$\overrightarrow{AB}$,$\overrightarrow{AN}$=n$\overrightarrow{AC}$,则( )
在△ABC中,点D在线段BC上,且满足BD=$\frac{1}{2}$DC,过点D的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AM}$=m$\overrightarrow{AB}$,$\overrightarrow{AN}$=n$\overrightarrow{AC}$,则( )| A. | m+n是定值,定值为2 | B. | 2m+n是定值,定值为3 | ||
| C. | $\frac{1}{m}$+$\frac{1}{n}$是定值,定值为2 | D. | $\frac{2}{m}$+$\frac{1}{n}$是定值,定值为3 |
分析 根据条件$\overrightarrow{AM}=m\overrightarrow{AB}$便得到$\overrightarrow{DM}-\overrightarrow{DA}=m(\overrightarrow{DB}-\overrightarrow{DA})$,从而得到$\overrightarrow{DB}=\frac{1}{m}\overrightarrow{DM}+(1-\frac{1}{m})\overrightarrow{DA}$,同理可由条件$\overrightarrow{AN}=n\overrightarrow{AC}$得到$\overrightarrow{DC}=\frac{1}{n}\overrightarrow{DN}+(1-\frac{1}{n})\overrightarrow{DA}$,这样由$\overrightarrow{DC}=-2\overrightarrow{DB}$,及$\overrightarrow{DM}$∥$\overrightarrow{DN}$即可得到1$-\frac{1}{n}=-2(1-\frac{1}{m})$,从而得到$\frac{2}{m}+\frac{1}{n}=3$,从而选项D正确.
解答  解:连接DA,由$\overrightarrow{AM}=m\overrightarrow{AB}$得:
解:连接DA,由$\overrightarrow{AM}=m\overrightarrow{AB}$得:
$\overrightarrow{DM}-\overrightarrow{DA}=m\overrightarrow{DB}-m\overrightarrow{DA}$;
∴$\overrightarrow{DB}=\frac{1}{m}\overrightarrow{DM}+(1-\frac{1}{m})\overrightarrow{DA}$;
同理,由$\overrightarrow{AN}=n\overrightarrow{AC}$:$\overrightarrow{DN}-\overrightarrow{DA}=n\overrightarrow{DC}-n\overrightarrow{DA}$;
∴$\overrightarrow{DC}=\frac{1}{n}\overrightarrow{DN}+(1-\frac{1}{n})\overrightarrow{DA}$;
∵$BD=\frac{1}{2}DC$;
∴DC=2BD;
∴$\overrightarrow{DC}=-2\overrightarrow{DB}$;
∴$\frac{1}{n}\overrightarrow{DN}+(1-\frac{1}{n})\overrightarrow{DA}=\frac{-2}{m}\overrightarrow{DM}$$-2(1-\frac{1}{m})\overrightarrow{DA}$;
$\overrightarrow{DM}$和$\overrightarrow{DN}$共线,∴存在实数λ,使$\overrightarrow{DM}=λ\overrightarrow{DN}$;
∴$\frac{1}{n}\overrightarrow{DN}+(1-\frac{1}{n})\overrightarrow{DA}$=$-\frac{2λ}{m}\overrightarrow{DN}+(-2+\frac{2}{m})\overrightarrow{DA}$;
∴$1-\frac{1}{n}=-2+\frac{2}{m}$;
∴$\frac{1}{n}+\frac{2}{m}=3$;
∴$\frac{2}{m}+\frac{1}{n}$是定值,定值为3.
故选:D.
点评 考查向量减法的几何意义,共线向量基本定理,以及平面向量基本定理.


科目:高中数学 来源: 题型:选择题
| A. | -4<a≤2 | B. | -4≤a<2 | C. | a≤4 | D. | a≥-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
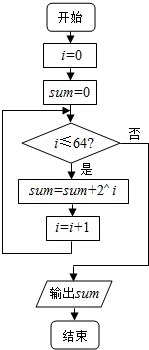
| A. | 求和S=2+22+…+264 | B. | 求和S=1+2+22+…+263 | ||
| C. | 求和S=1+2+22+…+264 | D. | 以上均不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com