
 设函数f(x)=|x2-2x-3|.
设函数f(x)=|x2-2x-3|.分析 (1)f(x)=|x2-2x-3|=0,可得函数f(x)的零点;
(2)去掉绝对值,原函数变成:f(x)=|x2-2x-3|=$\left\{\begin{array}{l}{-{x}^{2}+2x+3=-(x-1)^{2}+4,-1≤x≤3}\\{{x}^{2}-2x-3=(x-1)^{2}-4,x<-1或x>3}\end{array}\right.$,画出每段上的二次函数图象,根据图象即可写出单调区间.
解答 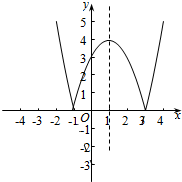 解:(1)f(x)=|x2-2x-3|=0,∴x=-1或3.
解:(1)f(x)=|x2-2x-3|=0,∴x=-1或3.
(2)f(x)=|x2-2x-3|=$\left\{\begin{array}{l}{-{x}^{2}+2x+3=-(x-1)^{2}+4,-1≤x≤3}\\{{x}^{2}-2x-3=(x-1)^{2}-4,x<-1或x>3}\end{array}\right.$.
∴图象为:
通过图象可以看出单调增区间为:[-1,1],(3,+∞);单调减区间为:(-∞,-1),(1,3].
点评 本题主要考查含绝对值函数图象的画法及通过图形求单调区间的方法,属于中档题.


科目:高中数学 来源: 题型:解答题
| 类别 | 1号广告 | 2号广告 | 3号广告 | 4号广告 |
| 广告次数 | 20 | 30 | 40 | 10 |
| 时间t(分钟/人) | 2 | 3 | 4 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四边形ABCD中,AD∥BC,BC=CD,∠ADC=90°,BC=DC=2AD,E为四边形ABCD内一点,F为四边形ABCD外一点,且∠BEC=∠DFC=90°,BE∥CF交CD的中点于N.
在四边形ABCD中,AD∥BC,BC=CD,∠ADC=90°,BC=DC=2AD,E为四边形ABCD内一点,F为四边形ABCD外一点,且∠BEC=∠DFC=90°,BE∥CF交CD的中点于N.查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:选择题
在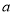 和
和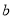 两数之间插入5个数,使他们与
两数之间插入5个数,使他们与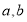 组成等差数列,则该数列的公差为( )
组成等差数列,则该数列的公差为( )
A.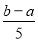 B.
B.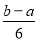 C.
C.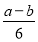 D.
D.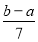
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行 | B. | 垂直 | C. | 平行或重合 | D. | 相交且不垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com