【题目】在
中，角
所对的边分别为
，已知
.
（1）求证：
成等差数列；
（2）若
，的面积为
，求
.
【答案】(1)证明见解析；(2)4.
【解析】试题分析：
(1)结合题意首先利用正弦定理边化角，结合两角和差正余弦公式进行化简，然后再角化边即可证得题中的结论；
(2)由余弦定理得到关于边c的方程，解方程即可求得边长的值.
试题解析：
（1）∵b（1+cosC）=c（2-cosB），
∴由正弦定理可得：sinB+sinBcosC=2sinC-sinCcosB，可得：sinBcosC+sinCcosB+sinB=2sinC，
∴sinA+sinB=2sinC，
∴a+b=2c，即a，c，b成等差数列；
（2）∵C=
，△ABC的面积为4
=
absinC=
ab，
∴ab=16，
∵由余弦定理可得：c2=a2+b2-2abcosC=a2+b2-ab=（a+b）2-3ab，
∵a+b=2c，
∴可得：c2=4c2-3×16，解得：c=4.
科目：高中数学 来源： 题型：
【题目】 用总长14.8米的钢条制作一个长方体容器的框架，如果所制容器底面一边的长比另一边的长多0.5米，那么高为多少时容器的容积最大？最大容积是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数列{an}中，a1=8，a4=2，且满足an+2﹣2an+1+an=0，n∈N* ．
（1）求数列{an}的通项；
（2）设Sn=|a1|+|a2|+…+|an|，求Sn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某研究型学习小组调查研究”中学生使用智能手机对学习的影响”．部分统计数据如下表:
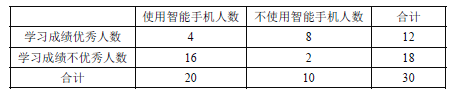
参考数据:
参考公式: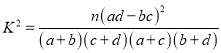 
，其中
(Ⅰ)试根据以上数据，运用独立性检验思想，指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为
组，不使用智能手机且成绩优秀的8位同学记为
组，计划从
组推选的2人和
组推选的3人中，随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验．求挑选的两人恰好分别来自
、
两组的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
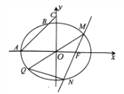
【题目】已知椭圆
： 
的左顶点为
，右焦点为
，过点
且斜率为1的直线交椭圆
于另一点
，交
轴于点
， 
．
（1）求椭圆
的方程；
（2）过点
作直线
与椭圆
交于
两点，连接
（
为坐标原点）并延长交椭圆
于点
，求
面积的最大值及取最大值时直线
的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念．记交通指数为
，其范围为
，分别有5个级别：
畅通；
基本畅通；
轻度拥堵；
中度拥堵；
严重拥堵．早高峰时段（
），从贵阳市交通指挥中心随机选取了二环以内50个交通路段，依据交通指数数据绘制的直方图如图所示：
（1）据此直方图估算交通指数
时的中位数和平均数；
（2）据此直方图求出早高峰二环以内的3个路段至少有两个严重拥堵的概率是多少？
（3）某人上班路上所用时间若畅通时为20分钟，基本畅通为30分钟，轻度拥堵为35分钟，中度拥堵为45分钟，严重拥堵为60分钟，求此人所用时间的数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）是定义在R上的偶函数，当x≥0时，f（x）=x2﹣2x﹣1．
（1）求f（x）的函数解析式，并用分段函数的形式给出；
（2）作出函数f（x）的简图；
（3）写出函数f（x）的单调区间及最值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4．
（1）从袋中随机抽取两个球，求取出的球的编号之和不大于4的概率；
（2）先从袋中随机取一个球，该球的编号为m，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n，求n＜m+2的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
