
分析 利用正弦定理把题设中关于边的等式转换成角的正弦,进而利用两角差公式化简整理求得A=B,进而求得a=b.根据余弦定理求得a,b,进而利用三角形面积公式即可得解.
解答 解:∵acosB=bcosA,且C=120°,c=2$\sqrt{3}$,
∴由题意及正弦定理可得:sinAcosB=sinBcosA,
即sin(A-B)=0,故A=B,由正弦定理可得:a=b,
∴由余弦定理c2=a2+b2-2abcosC可得:12=a2+a2-2×a×a×cos120°,解得a=b=2.
∴△ABC的面积S=$\frac{1}{2}$absinC=$\frac{1}{2}×2×2×sin120°$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题主要考查了余弦定理的应用,正弦定理的应用,两角和公式的化简求值,属于基本知识的考查.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
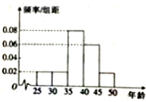 2015年某企业员工有500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.现在要从年龄较小的第1,3,4组中用分层抽样的方法抽取16人,则在第4组抽取的人数为( )
2015年某企业员工有500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.现在要从年龄较小的第1,3,4组中用分层抽样的方法抽取16人,则在第4组抽取的人数为( )| A. | 3 | B. | 6 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 0.5 | 0.53125 | 0.5625 | 0.625 | 0.75 | 1 |
| f(x) | -1.307 | -0.084 | -0.009 | 0.066 | 0.215 | 0.512 | 1.099 |
| A. | 0.625 | B. | -0.009 | C. | 0.5625 | D. | 0.066 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
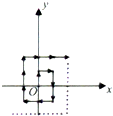 如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )| A. | (-21,12) | B. | (-22,12) | C. | (-21,13) | D. | (-22,13) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com