
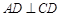 ,
,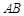 ∥
∥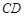 ,
,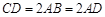 .
.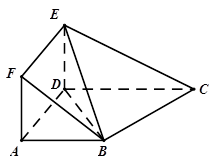
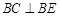 ;
; 与平面
与平面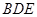 所成角的正切值;
所成角的正切值;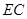 上找一点
上找一点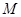 ,使得
,使得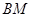 ∥平面ADEF,请确定M点的位置,并给出证明.
∥平面ADEF,请确定M点的位置,并给出证明.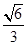 .(3)M是EC中点,BM∥面ADEF.
.(3)M是EC中点,BM∥面ADEF.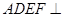 面
面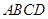 ,
,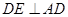 ,得到
,得到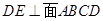 ,
,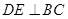 .
.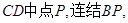 四边形
四边形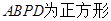 .
.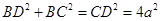 ,得到
,得到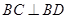 ,
,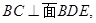 证得
证得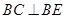 .
.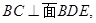
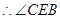 即为CE与面BDE所成的角.
即为CE与面BDE所成的角. 中,可得
中,可得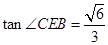 .
.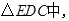 由三角形中位线定理,可得
由三角形中位线定理,可得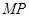 ∥
∥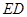 ,进一步可得证.
,进一步可得证.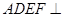 面
面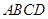 ,面
,面 面
面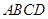
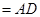 .
.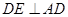 ,
, ,
,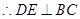 .
.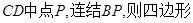
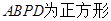 .
.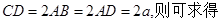
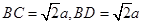 ,
,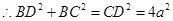 ,
,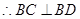 ,
,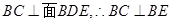 . 4分
. 4分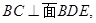
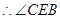 即为CE与面BDE所成的角.
即为CE与面BDE所成的角. 中,
中,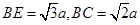 ,
,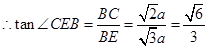 . 8分
. 8分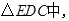 M、P分别为EC、DC的中点,
M、P分别为EC、DC的中点,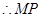 ∥
∥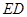 ,∴MP∥面ADEF,∴面BMP∥面ADEF,∴BM∥面ADEF. 12分
,∴MP∥面ADEF,∴面BMP∥面ADEF,∴BM∥面ADEF. 12分

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 AB.Q是PC上的一点.
AB.Q是PC上的一点.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
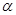 内的两条不同直线,l是平面
内的两条不同直线,l是平面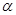 外的一条直线,则
外的一条直线,则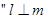 且
且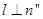 是
是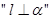 的( )
的( )| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
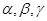 是三个不重合的平面,
是三个不重合的平面, 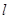 是直线,给出下列四个命题:①若
是直线,给出下列四个命题:①若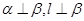 则
则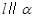 ;②若
;②若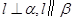 则
则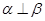 ;③若
;③若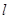 上有两点到
上有两点到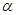 的距离相等,则
的距离相等,则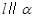 ;④若
;④若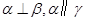 ,则
,则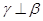 其中正确命题的序号 ( )
其中正确命题的序号 ( )| A.②④ | B.①④ | C.②③ | D.①② |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
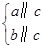 a∥b;②
a∥b;②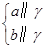 a∥b;③
a∥b;③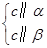 α∥β;
α∥β;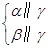 α∥β;⑤
α∥β;⑤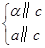 α∥a;⑥
α∥a;⑥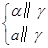 a∥α.
a∥α.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com