
【题目】将函数 ![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的 ![]() ,纵坐标不变,再向右平移
,纵坐标不变,再向右平移 ![]() 个单位长度,得到函数y=g(x)的图象,则下列说法正确的是( )
个单位长度,得到函数y=g(x)的图象,则下列说法正确的是( )
A.函数g(x)的一条对称轴是 ![]()
B.函数g(x)的一个对称中心是 ![]()
C.函数g(x)的一条对称轴是 ![]()
D.函数g(x)的一个对称中心是 ![]()
【答案】C
【解析】解:将函数 ![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的 ![]() , 可得y=2sin(2x+
, 可得y=2sin(2x+ ![]() )的图象,
)的图象,
然后纵坐标不变,再向右平移 ![]() 个单位长度,
个单位长度,
得到函数y=g(x)=2sin(2x﹣ ![]() +
+ ![]() )=2cos2x的图象,
)=2cos2x的图象,
令x= ![]() ,求得g(x)=0,
,求得g(x)=0,
可得( ![]() ,0)是g(x)的一个对称中心,故排除A;
,0)是g(x)的一个对称中心,故排除A;
令x= ![]() ,求得g(x)=﹣1,
,求得g(x)=﹣1,
可得x= ![]() 是g(x)的图象的一条对称轴,故排除B,故C正确;
是g(x)的图象的一条对称轴,故排除B,故C正确;
令x= ![]() ,求得g(x)=
,求得g(x)= ![]() ,可得x=
,可得x= ![]() 不是g(x)的图象的对称中心,故排除D,
不是g(x)的图象的对称中心,故排除D,
故选:C.
【考点精析】解答此题的关键在于理解函数y=Asin(ωx+φ)的图象变换的相关知识,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA. 
(1)求证:BE⊥平面PAC;
(2)求直线AB与平面BEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年春晚过后,为了研究演员上春晚次数与受关注度的关系,某网站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计,得到如下数据:
上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
粉丝数量y(单位:万人) | 10 | 20 | 40 | 80 | 100 |
(1)若该演员的粉丝数量g(x)≤g(1)=0与上春晚次数x满足线性回归方程,试求回归方程 ![]() =
= ![]() x+
x+ ![]() ,并就此分析,该演员上春晚12次时的粉丝数量;
,并就此分析,该演员上春晚12次时的粉丝数量;
(2)若用 ![]() (i=1,2,3,4,5)表示统计数据时粉丝的“即时均值”(四舍五入,精确到整数),从这5个“即时均值”中任选2数,记所选的2数之和为随机变量η,求η的分布列与数学期望. 参考公式:
(i=1,2,3,4,5)表示统计数据时粉丝的“即时均值”(四舍五入,精确到整数),从这5个“即时均值”中任选2数,记所选的2数之和为随机变量η,求η的分布列与数学期望. 参考公式: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=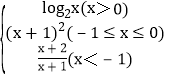 ,若对任意给定的m∈(1,+∞),都存在唯一的x0∈R满足f(f(x0))=2a2m2+am,则正实数a的取值范围为( )
,若对任意给定的m∈(1,+∞),都存在唯一的x0∈R满足f(f(x0))=2a2m2+am,则正实数a的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂用鲜牛奶在某台设备上生产A,B两种奶制品.生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A,B两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
W | 12 | 15 | 18 |
P | 0.3 | 0.5 | 0.2 |
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利Z(单位:元)是一个随机变量.
(1)求Z的分布列和均值;
(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且![]() ,若任意的
,若任意的![]() ,当
,当![]() 时,总有
时,总有![]() .
.
(1)判断函数![]() 在[-1,1]上的单调性,并证明你的结论;
在[-1,1]上的单调性,并证明你的结论;
(2)解不等式:![]() ;
;
(3)若![]() 对所有的
对所有的![]() 恒成立,其中
恒成立,其中![]() (
(![]() 是常数),求实数
是常数),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果对一切实数x、y,不等式 ![]() ﹣cos2x≥asinx﹣
﹣cos2x≥asinx﹣ ![]() 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.(﹣∞, ![]() ]
]
B.[3,+∞)
C.[﹣2 ![]() ,2
,2 ![]() ]
]
D.[﹣3,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是不小于3的正整数,集合
是不小于3的正整数,集合![]() ,对于集合
,对于集合![]() 中任意两个元素
中任意两个元素![]() ,
,![]() .
.
定义1:![]() .
.
定义2:若![]() ,则称
,则称![]() ,
,![]() 互为相反元素,记作
互为相反元素,记作![]() ,或
,或![]() .
.
(Ⅰ)若![]() ,
,![]() ,
,![]() ,试写出
,试写出![]() ,
,![]() ,以及
,以及![]() 的值;
的值;
(Ⅱ)若![]() ,证明:
,证明:![]() ;
;
(Ⅲ)设![]() 是小于
是小于![]() 的正奇数,至少含有两个元素的集合
的正奇数,至少含有两个元素的集合![]() ,且对于集合
,且对于集合![]() 中任意两个不相同的元素
中任意两个不相同的元素![]() ,
,![]() ,都有
,都有![]() ,试求集合
,试求集合![]() 中元素个数的所有可能值.
中元素个数的所有可能值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com