【题目】有一座大桥既是交通拥挤地段，又是事故多发地段，为了保证安全，交通部门规定：大桥上的车距d（m）与车速v（km/h）和车身长l（m）的关系满足：d=kv2l+ 
l（k为正的常数），假定大桥上的车的车身长都为4m，当车速为60km/h时，车距为2.66个车身长．
（1）写出车距d关于车速v的函数关系式；
（2）应规定怎样的车速，才能使大桥上每小时通过的车辆最多？
【答案】
（1）解：因为当v=60时，d=2.66l，所以 
，
∴d=0.0024v2+2
（2）解：设每小时通过的车辆为Q，每小时内通过汽车的数量为Q最大，只须 
最小，
即Q= 
∵ 
，
当且仅当 
，即v=50时，Q取最大值 
．
答：当v=50（km/h）时，大桥每小时通过的车辆最多
【解析】（1）根据当车速为60（km/h）时，车距为2.66个车身长，建立等式关系，求出k的值，即可求出车距d关于车速v的函数关系式；（2）设每小时通过的车辆为Q，每小时内通过汽车的数量为Q最大，只须 最小，将d代入，然后利用基本不等式求出最值，即可求出所求．
【考点精析】解答此题的关键在于理解基本不等式的相关知识，掌握基本不等式：
,（当且仅当
时取到等号）；变形公式：
．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
，g（x）=f（x）﹣a
（1）当a=2时，求函数g（x）的零点；
（2）若函数g（x）有四个零点，求a的取值范围；
（3）在（2）的条件下，记g（x）得四个零点分别为x1 ， x2 ， x3 ， x4 ， 求x1+x2+x3+x4的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，内角A、B、C所对的边分别是a、b、c，且a+b+c=8． （Ⅰ）若a=2，b= 
，求cosC的值；
（Ⅱ）若sinAcos2 
+sinBcos2 
=2sinC，且△ABC的面积S= 
sinC，求a和b的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】袋中有质地、大小完全相同的5个小球，编号分别为1，2，3，4，5，甲、乙两人玩一种游戏．甲先摸出一个球．记下编号，放回后再摸出一个球，记下编号，如果两个编号之和为偶数．则算甲赢，否则算乙赢．
（1）求甲赢且编号之和为6的事件发生的概率：
（2）试问：这种游戏规则公平吗．请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】根据题意解答
（1）利用“五点法”画出函数 
在长度为一个周期的闭区间的简图．
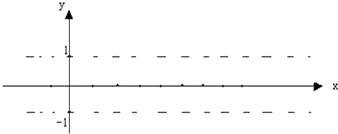
（2）并说明该函数图像可由y=sinx（x∈R）的图像经过怎样平移和伸缩变换得到的．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校为缓解高三学生的高考压力，经常举行一些心理素质综合能力训练活动，经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试，并将其成绩分为
、
、
、
、
五个等级，统计数据如图所示（视频率为概率），根据以上抽样调查数据，回答下列问题：
（1）试估算该校高三年级学生获得成绩为
的人数；
（2）若等级
、
、
、
、
分别对应100分、90分、80分、70分、60分，学校要求平均分达90分以上为“考前心理稳定整体过关”，请问该校高三年级目前学生的“考前心理稳定整体”是否过关？
（3）为了解心理健康状态稳定学生的特点，现从
、
两种级别中，用分层抽样的方法抽取11个学生样本，再从中任意选取3个学生样本分析，求这3个样本为
级的个数
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
