练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

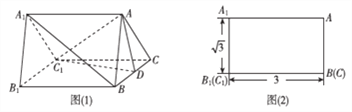
    【题目】如图(1)是一个水平放置的正三棱柱， 是棱的中点，正三棱柱的主视图如图(2).

    (1)图(1)中垂直于平面的平面有哪几个(直接写出符合要求的平面即可，不必说明或证明)

    (2)求正三棱柱的体积；

    (3)证明： 平面.

    【答案】（1）详见解析；（2）；（3）详见解析.

    【解析】试题分析：（1）由于几何体为正三棱柱，故两个底面和侧面垂直，由于平面，所以面也和平面垂直.（2）先计算得底面边长为，由三视图可知高为，由此求得几何体的体积.（3）连接交于，连接，利用三角形的中位线证明，从而证明线面平行.

    试题解析：

    （1）平面、平面、平面

    （2）依题意，在正三棱柱中， 从而.

    所以正三棱柱的体积 .

    （3）连接设连接.

    因为是正三棱柱的侧面，所以是矩形， 是的中点.

    所以是的中位线,

    因为平面平面,所以平面

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知曲线 上有一点列过点在x轴上的射影是，且1＋2＋3＋…＋n＝2n+1－n－2. （n∈N*）

    （1）求数列{}的通项公式

    （2）设四边形 的面积是，求

    （3）在（2）条件下，求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数为奇

    函数，且相邻两对称轴间的距离为.

    （Ⅰ）当时，求的单调递减区间；

    （Ⅱ）将函数的图象沿轴方向向右平移个单位长度，再把横坐标缩短到原来的（纵坐标不变），

    得到函数的图象.当时，求函数的值域.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设p:实数x满足,其中,命题实数满足

    |x-3|≤1 .

    (1)若且为真，求实数的取值范围；

    (2)若是的充分不必要条件,求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在四棱锥中,底面为平行四边形, 为侧棱的中点.

    （Ⅰ）求证: ∥平面

    （Ⅱ）若,,

    求证:平面平面

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正三棱柱中，，，点为的中点，点在线段上．

    （1）当时，求证：；

    （2）是否存在点，使二面角等于？若存在，求的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大学餐饮中心为了了解新生的饮食习惯，利用简单随机抽样的方法在全校一年级学生中进行了抽样调查，调查结果如下表所示：

    喜欢甜品

    不喜欢甜品

    合计

    南方学生

    60

    20

    80

    北方学生

    10

    10

    20

    合计

    70

    30

    100

    （1）根据表中数据，问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”；

    （2）根据（1）的结论，你能否提出更好的调查方法来了解该校大学新生的饮食习惯，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （1）求不等式的解集；

    （2）若对一切，均有成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图，将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性.

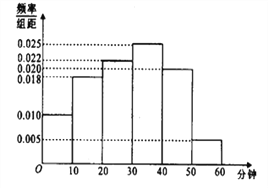
    （Ⅰ）根据已知条件完成下面的列联表，并据此资料判断你是否有95％以上的把握认为“体育迷”与性别有关?

    非体育迷

    体育迷

    合计

    男

    女

    合计

    （参考公式，其中.）

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    （Ⅱ）将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率。

    查看答案和解析>>

    同步练习册答案