
(本大题10分)求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程
(1)与直线2x + y + 5 = 0平行 ;
(2)与直线2x + y + 5 = 0垂直;
(1) ;(2)
;(2) 。
。
【解析】
试题分析:先通过两直线方程联立解方程组求出交点坐标.(1)根据两直线平行,斜率相等,设出所求直线方程,将交点坐标代入即可求出平行直线的方程.
(2)根据两直线垂直,斜率之积等于-1,设出所求直线的斜截式方程,然后将交点坐标代入所求直线的方程,即可得解.
 解得
解得 --------2分
--------2分
所以交点(-1,2)
(1) -----4分
-----4分
直线方程为 --------6分
--------6分
(2) ---------8分
---------8分
直线方程为 --------10分.
--------10分.
考点:两直线平行与垂直的判定..
点评:两直线平行:斜率都不存在或斜率相等.两直线垂直:斜率之积等于-1或一条直线的斜率不存在,另一条斜率等于0.


科目:高中数学 来源:2011年山东省济南外国语学校高一入学检测数学试卷 题型:解答题
((本小题12分)
经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天) 的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20-
的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20-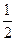 |t-10|.
|t-10|.
(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(2)求该种商品的日销售额y的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省汕头市高三上学期期中文科数学试卷(解析版) 题型:解答题
(本小题满分14分)某种商品的成本为5元/ 件,开始按8元/件销售,销售量为50件,为了获得最大利润,商家先后采取了提价与降价两种措施进行试销。经试销发现:销售价每上涨1元每天销售量就减少10件;而降价后,日销售量Q(件)与实际销售价x(元)满足关系:
|
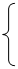
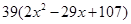
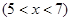 [
[
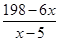
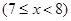 [
[
(1)求总利润(利润=销售额-成本)y(元)与销售价x(件)的函数关系式;
(2)试问:当实际销售价为多少元时,总利润最大.
查看答案和解析>>
科目:高中数学 来源:2011年山东省高一入学检测数学试卷 题型:解答题
((本小题12分)
经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20- |t-10|.
|t-10|.
(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(2)求该种商品的日销售额y的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三学情调研考试数学卷 题型:解答题
(本小题满分14分)
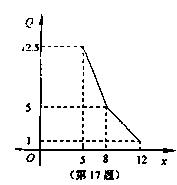
某专卖店经市场调查得知,一种商品的月销售量Q(单位:吨)与销售价格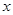 (单位:万元/吨)的关系可用下图的一条折线表示.
(单位:万元/吨)的关系可用下图的一条折线表示.
(1)写出月销售量Q关于销售价格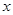 的函数关系;
的函数关系;
(2)如果该商品的进价为5万元/吨,除去进货成本外,专卖店销售该商品每月的固定成本为10万元,问该商品每吨定价多少万元时,销售该商品的月利润最大?并求月利润的最大值.
查看答案和解析>>
科目:高中数学 来源:2010年山西省临汾市高一年级学段考试数学试卷 题型:解答题
(本小题满分10分)
某公司试销一种新产品,规定试销时销售单价不低于成本单价500元/件,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价 (元/件),可近似看做一次函数
(元/件),可近似看做一次函数 的关系(图象如下图所示).
的关系(图象如下图所示).
(1)根据图象,求一次函数 的表达式;
的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元,
①求S关于 的函数表达式;
的函数表达式;
②求该公司可获得的最大毛利润,并求出此时相应的销售单价.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com