
| S | 2甲 |
| S | 2乙 |
| 1 |
| n |
| . |
| x |
| . |
| x |
| . |
| x |
| . |
| x |
| . |
| x甲 |
| 1 |
| 5 |
| . |
| x乙 |
| 1 |
| 5 |
| S | 2甲 |
| 1 |
| 5 |
| S | 2乙 |
| 1 |
| 5 |
| . |
| x甲 |
| . |
| x乙 |
| 5 |
| 25 |
| 1 |
| 5 |


科目:高中数学 来源: 题型:
| 1号 | 2号 | 3号 | 4号 | 5号 | |
| 甲组 | 4 | 5 | 7 | 9 | 10 |
| 乙组 | 5 | 6 | 7 | 8 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
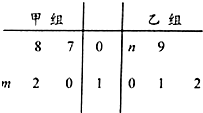
 某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.| S | 2 甲 |
| S | 2 乙 |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示,已知两组技工在单位时间内加工的合格零件数的平均数都为10.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示,已知两组技工在单位时间内加工的合格零件数的平均数都为10. | S | 2 甲 |
| S | 2 乙 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省深圳高级中学高三(上)期末数学试卷(文科)(解析版) 题型:解答题
| 1号 | 2号 | 3号 | 4号 | 5号 | |
| 甲组 | 4 | 5 | 7 | 9 | 10 |
| 乙组 | 5 | 6 | 7 | 8 | 9 |
查看答案和解析>>
科目:高中数学 来源:2010年福建省厦门市高三3月质量检查数学试卷(文科)(解析版) 题型:解答题
| 1号 | 2号 | 3号 | 4号 | 5号 | |
| 甲组 | 4 | 5 | 7 | 9 | 10 |
| 乙组 | 5 | 6 | 7 | 8 | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com