
【题目】对n个不同的实数a1,a2,…,an可得n!个不同的排列,每个排列为一行写成一个n!行的数阵.对第i行ai1,ai2,…,ain,记bi=-ai1+2ai2-3ai3+…+(-1)nnain,i=1,2,3…,n!.例如用1,2,3可得数阵如图,对于此数阵中每一列各数之和都是12,所以bl+b2+…b6=-12+2×12-3×12=-24.那么,在用1,2,3,4,5形成的数阵中,b1+b2+…b120等于( )

A.-3600B.-1800C.-1080D.-720
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是无穷数列.给出两个性质:
是无穷数列.给出两个性质:
①对于![]() 中任意两项
中任意两项![]() ,在
,在![]() 中都存在一项
中都存在一项![]() ,使
,使![]() ;
;
②对于![]() 中任意项
中任意项![]() ,在
,在![]() 中都存在两项
中都存在两项![]() .使得
.使得![]() .
.
(Ⅰ)若![]() ,判断数列
,判断数列![]() 是否满足性质①,说明理由;
是否满足性质①,说明理由;
(Ⅱ)若![]() ,判断数列
,判断数列![]() 是否同时满足性质①和性质②,说明理由;
是否同时满足性质①和性质②,说明理由;
(Ⅲ)若![]() 是递增数列,且同时满足性质①和性质②,证明:
是递增数列,且同时满足性质①和性质②,证明:![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》有这样一个问题:从冬至日起,依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸,雨水、惊蛰、春分、清明日影之和为三丈二尺,前七个节气日影之和为七丈三尺五寸,问立夏日影长为( )
A.七尺五寸B.六尺五寸C.五尺五寸D.四尺五寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体![]() 中,P为线段
中,P为线段![]() 上的动点,下列说法正确的是( )
上的动点,下列说法正确的是( )
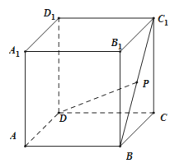
A.对任意点P,![]() 平面
平面![]()
B.三棱锥![]() 的体积为
的体积为![]()
C.线段DP长度的最小值为![]()
D.存在点P,使得DP与平面![]() 所成角的大小为
所成角的大小为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】Keep是一款具有社交属性的健身APP,致力于提供健身教学、跑步、骑行、交友及健身饮食指导、装备购买等一站式运动解决方案.Keep可以让你随时随地进行锻炼,记录你每天的训练进程.不仅如此,它还可以根据不同人的体质,制定不同的健身计划.小明根据Keep记录的2019年1月至2019年11月期间每月跑步的里程(单位:十公里)数据整理并绘制了下面的折线图.根据该折线图,下列结论正确的是( )
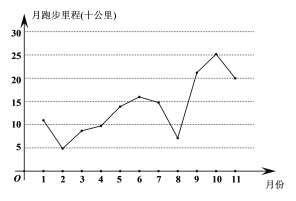
A.月跑步里程最小值出现在2月
B.月跑步里程逐月增加
C.月跑步里程的中位数为5月份对应的里程数
D.1月至5月的月跑步里程相对于6月至11月波动性更小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,
,![]() 、
、![]() 分别为椭圆长轴的左、右端点,
分别为椭圆长轴的左、右端点,![]() 为直线
为直线![]() 上异于点
上异于点![]() 的任意一点,连接
的任意一点,连接![]() 交椭圆于
交椭圆于![]() 点.
点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)是否存在![]() 轴上的定点
轴上的定点![]() 使得以
使得以![]() 为直径的圆恒过
为直径的圆恒过![]() 与
与![]() 的交点?如果存在,请求出定点
的交点?如果存在,请求出定点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (φ为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(φ为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为![]() ,曲线C1和C2在第一象限交于点A.
,曲线C1和C2在第一象限交于点A.
(1)求点A的直角坐标;
(2)直线![]() 与曲线C1,C2在第一象限分别交于点B,C,若△ABC的面积为
与曲线C1,C2在第一象限分别交于点B,C,若△ABC的面积为![]() ,求α的值.
,求α的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com