
【题目】设数列{an}:1,﹣2,﹣2,3,3,3,﹣4,﹣4,﹣4,﹣4,…, ![]() ,…,即当
,…,即当 ![]() <n≤
<n≤ ![]() (k∈N*)时,
(k∈N*)时, ![]() .记Sn=a1+a2+…+an(n∈N).对于l∈N , 定义集合Pl=﹛n|Sn为an的整数倍,n∈N , 且1≤n≤l}
.记Sn=a1+a2+…+an(n∈N).对于l∈N , 定义集合Pl=﹛n|Sn为an的整数倍,n∈N , 且1≤n≤l}
(1)求P11中元素个数;
(2)求集合P2000中元素个数.
【答案】
(1)
解:由数列{an}的定义得a1=1,a2=﹣2,a3=﹣2,a4=3,
a5=3,a6=3,a7=﹣4,a8=﹣4,a9=﹣4,a10=﹣4,a11=5,
所以S1=1,S2=﹣1,S3=﹣3,S4=0,S5=3,S6=6,S7=2,
S8=﹣2,S9=﹣6,S10=﹣10,S11=﹣5,
从而S1=a1,S4=0a4,S5=a5,S6=2a6,S11=﹣a11,
所以集合P11中元素的个数为5;
(2)
解:先证:Si(2i+1)=﹣i(2i+1)(i∈N*).
事实上,①当i=1时,Si(2i+1)=S3=﹣3,﹣i(2i+1)=﹣3,故原等式成立;
②假设i=m时成立,即Sm(2m+1)=﹣m(2m+1),则i=m+1时,
S(m+1)(2m+3)=Sm(2m+1)+(2m+1)2﹣(2m+2)2=﹣m(2m+1)﹣4m﹣3
=﹣(2m2+5m+3)=﹣(m+1)(2m+3).
综合①②可得Si(2i+1)=﹣i(2i+1).于是S(i+1)(2i+1)=Si(2i+1)+(2i+1)2
=﹣i(2i+1)+(2i+1)2=(2i+1)(i+1).
由上可知Si(2i+1)是2i+1的倍数,而ai(2i+1)+j=2i+1(j=1,2,…,2i+1),
所以Si(2i+1)+j=Si(2i+1)+j(2i+1)是ai(2i+1)+j(j=1,2,…,2i+1)的倍数.
又S(i+1)(2i+1)=(i+1)(2i+1)不是2i+2的倍数,
而a(i+1)(2i+1)+j=﹣(2i+2)(j=1,2,…,2i+2),
所以S(i+1)(2i+1)+j=S(i+1)(2i+1)+j(2i+2)=(2i+1)(i+1)﹣j(2i+2)
不是a(i+1)(2i+1)+j(j=1,2,…,2i+2)的倍数,
故当l=i(2i+1)时,集合Pl中元素的个数为1+3+…+(2i﹣1)=i2,
于是,当l=i(2i+1)+j(1≤j≤2i+1)时,集合Pl中元素的个数为i2+j.
又2000=31×(2×31+1)+47,
故集合P2 000中元素的个数为312+47=1008.
【解析】(1)由数列{an}的定义,可得前11项,进而得到前11项和,再由定义集合Pl , 即可得到元素个数;(2)运用数学归纳法证明Si(2i+1)=﹣i(2i+1)(i∈N*).再结合定义,运用等差数列的求和公式,即可得到所求.
【考点精析】通过灵活运用数学归纳法的定义,掌握数学归纳法是证明关于正整数n的命题的一种方法即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知抛物线C1:x2=2py(p>0),点A(p, ![]() )到抛物线C1的准线的距离为2.
)到抛物线C1的准线的距离为2.
(1)求抛物线C1的方程;
(2)过点A作圆C2:x2+(y﹣a)2=1的两条切线,分别交抛物线于M,N两点,若直线MN的斜率为﹣1,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励市民节约用电,实行“阶梯式”电价,某边远山区每户居民月用电量划分为三档:月用电量不超过150度,按0.6元/度收费,超过150度但不超过250度的部分每度加价0.1元,超过250度的部分每度再加价0.3元收费.
(1)求该边远山区某户居民月用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)已知该边远山区贫困户的月用电量![]() (单位:度)与该户长期居住的人口数
(单位:度)与该户长期居住的人口数![]() (单位:人)间近似地满足线性相关关系:
(单位:人)间近似地满足线性相关关系:![]() (
(![]() 的值精确到整数),其数据如表:
的值精确到整数),其数据如表:
| 14 | 15 | 17 | 18 |
| 161 | 168 | 191 | 200 |
现政府为减轻贫困家庭的经济负担,计划对该边远山区的贫困家庭进行一定的经济补偿,给出两种补偿方案供选择:一是根据该家庭人数,每人每户月补偿6元;二是根据用电量每人每月补偿![]() (
(![]() 为用电量)元,请根据家庭人数
为用电量)元,请根据家庭人数![]() 分析,一个贫困家庭选择哪种补偿方式可以获得更多的补偿?
分析,一个贫困家庭选择哪种补偿方式可以获得更多的补偿?
附:回归直线![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某一部件由四个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3或元件4正常工作,则部件正常工作.设四个电子元件的使用寿命(单位:小时)均服从正态分布![]() ,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.
,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,2a9=a12+13,a3=7,其前n项和为Sn.
(1)求数列{an}的通项公式;
(2)求数列{![]() }的前n项和Tn,并证明Tn<
}的前n项和Tn,并证明Tn<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足S=![]() (a2+c2﹣b2).
(a2+c2﹣b2).
(1)求角B的大小;
(2)若边b=![]() ,求a+c的取值范围.
,求a+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”.如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”.某地有三个新建居民区,分别位于平面xOy内三点A(3,20),B(﹣10,0),C(14,0)处.现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心.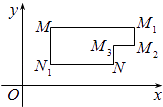
(1)写出点P到居民区A的“L路径”长度最小值的表达式(不要求证明);
(2)若以原点O为圆心,半径为1的圆的内部是保护区,“L路径”不能进入保护区,请确定点P的位置,使其到三个居民区的“L路径”长度之和最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com