Question

9．如图，在棱长为1的正方体ABCD-A₁B₁C₁D₁中，E为AB的中点．求：
（1）异面直线BD₁与CE所成角的余弦值；
（2）点A到平面A₁EC的距离．

Answer 1

分析 （1）延长DC至G，使CG=$\frac{1}{2}$DC，连结BG、D₁G，得出四边形EBGC是平行四边形，找出∠D₁BG就是异面直线BD₁与CE所成的角，求出它的余弦值；
（2）过A₁作A₁H⊥CE，交CE的延长线于H．连结AH，求出AH的值，再利用等积法求出点A到平面A₁EC的距离．

解答 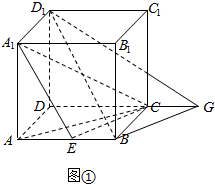解：（1）如图①所示；
延长DC至G，使CG=$\frac{1}{2}$DC，连结BG、D₁G，
CG∥EB，且CG=EB，∴四边形EBGC是平行四边形；
∴BG∥EC，
∴∠D₁BG就是异面直线BD₁与CE所成的角；
又△D₁BG中，D₁B=$\sqrt{3}$，
$\begin{array}{l}BG=\frac{{\sqrt{5}}}{2}，{D_1}G=\sqrt{{1^2}+（\frac{3}{2}{）^2}}=\frac{{\sqrt{13}}}{2}\\∴cos∠{D_1}BG=\frac{{{D_1}{B^2}+B{G^2}-{D_1}{G^2}}}{{2{D_1}B•BG}}=\frac{{3+\frac{5}{4}-\frac{13}{4}}}{{2×\frac{{\sqrt{15}}}{2}}}=\frac{{\sqrt{15}}}{15}\end{array}$；
即异面直线BD₁与CE所成角的余弦值是$\frac{\sqrt{15}}{15}$；
（2）如图②所示；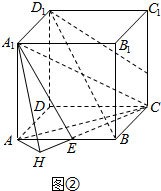
过A₁作A₁H⊥CE，交CE的延长线于H．连结AH，
在底面ABCD中，∵∠AHE=∠CBE=90°，∠AEH=∠CEB，
则△AHE∽△CBE，
∴$\frac{AH}{CB}$=$\frac{AE}{CE}$，且CE=$\frac{\sqrt{5}}{2}$，AE=$\frac{1}{2}$，
∴AH=$\frac{CB•AE}{CE}$=$\frac{1×\frac{1}{2}}{\frac{\sqrt{5}}{2}}$=$\frac{1}{\sqrt{5}}$；
在直角△A₁AH中，A₁A=1，AH=$\frac{1}{\sqrt{5}}$，∴A₁H=$\frac{\sqrt{6}}{\sqrt{5}}$；
设点A到平面A₁EC的距离为d，由三棱锥体积公式可得：
$\frac{1}{3}A{A_1}•{S_{△ACE}}=\frac{1}{3}d•{S_{△{A_1}CE}}$，
即$\frac{1}{3}•1•\frac{1}{2}•\frac{1}{2}•1=\frac{1}{3}d•\frac{1}{2}•\sqrt{\frac{1}{4}+1}•\frac{{\sqrt{6}}}{{\sqrt{5}}}$；
解得$d=\frac{{\sqrt{6}}}{6}$，
即点A到平面A₁EC的距离为$\frac{{\sqrt{6}}}{6}$．

点评 本题考查了空间中的点、线、面的位置关系以及空间想象能力与计算能力，解题时找角是关键，是综合性题目．