
����Ŀ�����������У���ȷ��������__________��
�ٻع�ֱ��![]() ��������������
��������������![]() �������ٹ�һ�������㣻
�������ٹ�һ�������㣻
�ڽ�һ�����ݵ�ÿ�����ݶ���һ����ͬ�ij�������䣻
�������ָ��![]() ������ع�Ч������ʾԤ�������Խ��ͱ����仯�Ĺ����ʣ�Խ�ӽ���1��˵��ģ�͵����Ч��Խ�ã�
������ع�Ч������ʾԤ�������Խ��ͱ����仯�Ĺ����ʣ�Խ�ӽ���1��˵��ģ�͵����Ч��Խ�ã�
�����������![]() ��
��![]() ���������
���������![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]() Խ����
Խ����![]() ��
��![]() ��ء��Ŀ��ų̶�ԽС��
��ء��Ŀ��ų̶�ԽС��
��.�����Ա���![]() �������
�������![]() ����
����![]() ȡֵһ��ʱ��
ȡֵһ��ʱ�� ![]() ��ȡֵ����һ��������ԣ�
��ȡֵ����һ��������ԣ� ![]() ��
�� ![]() ������ַ�ȷ����ϵ����������ϵ��
������ַ�ȷ����ϵ����������ϵ��
�ޣ��в�ͼ�вв��ȽϾ��ȵĵ�����ˮƽ�Ĵ�״�����У�˵��ѡ�õ�ģ�ͱȽϺ��ʣ�
��.����ģ���вв�ƽ����ԽС��ģ����ϵ�Ч��Խ��.
���𰸡��ڢޢ�
���������ٻع�ֱ��![]() ��������������
��������������![]() �����Բ����κ�һ�������㣻
�����Բ����κ�һ�������㣻
����һ�������е�ÿ�����ݶ�����ͬһ���������ݷ��ʽ��֪����㲻����
�������ָ��![]() ������ع�Ч������ʾԤ�������Խ��ͱ����仯�Ĺ����ʣ�Խ�ӽ���0��˵��ģ�͵����Ч��Խ�ã�
������ع�Ч������ʾԤ�������Խ��ͱ����仯�Ĺ����ʣ�Խ�ӽ���0��˵��ģ�͵����Ч��Խ�ã�
�����������![]() ��
��![]() ���������
���������![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]() Խ����
Խ����![]() ��
��![]() ��ء��Ŀ��ų̶�Խ��
��ء��Ŀ��ų̶�Խ��
��.�����Ա���![]() �������
�������![]() ����
����![]() ȡֵһ��ʱ��
ȡֵһ��ʱ�� ![]() ��ȡֵ����һ��������ԣ�
��ȡֵ����һ��������ԣ� ![]() ��
�� ![]() ������ַ�ȷ����ϵ������ع�ϵ��
������ַ�ȷ����ϵ������ع�ϵ��
�ޣ��в�ͼ�вв��ȽϾ��ȵĵ�����ˮƽ�Ĵ�״�����У�˵��ѡ�õ�ģ�ͱȽϺ��ʣ�
��.����ģ���вв�ƽ����ԽС��ģ����ϵ�Ч��Խ��.
�ʴ�Ϊ���ڢޢ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˫����x2�� ![]() =1�����ҽ���ֱ�ΪF1��F2 �� ����P��˫�����ϣ��ҡ�F1PF2Ϊ��������Σ���|PF1|+|PF2|��ȡֵ��Χ�� ��
=1�����ҽ���ֱ�ΪF1��F2 �� ����P��˫�����ϣ��ҡ�F1PF2Ϊ��������Σ���|PF1|+|PF2|��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽������![]() ����Сֵ����ȷ��ȡ����Сֵʱx��ֵ.�б����£�
����Сֵ����ȷ��ȡ����Сֵʱx��ֵ.�б����£�
x | �� | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | �� |
y | �� | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | �� |
��۲����yֵ��xֵ�仯���ص㣬������µ�����.
����![]() �����䣨0��2���ϵݼ���
�����䣨0��2���ϵݼ���
����![]() ������ �ϵ���.
������ �ϵ���.
��![]() ʱ��
ʱ�� ![]() .
.
֤��������![]() �����䣨0��2���ݼ�.
�����䣨0��2���ݼ�.
˼��������![]() ʱ������ֵ�������ֵ������Сֵ����ʱxΪ��ֵ����ֱ�ӻش���������֤����
ʱ������ֵ�������ֵ������Сֵ����ʱxΪ��ֵ����ֱ�ӻش���������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
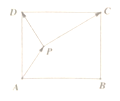
����Ŀ����ͼ����֪����![]() ��
�� ![]() ��
�� ![]() ����
����![]() Ϊ������һ�㣬��
Ϊ������һ�㣬��![]() ����
����![]() .
.
��1����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
��2����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn �� ����{ ![]() }�Ĺ���Ϊ1�ĵȲ����У���a2=3��a3=5��
}�Ĺ���Ϊ1�ĵȲ����У���a2=3��a3=5��
��1��������{an}��ͨ�ʽ��
��2����bn=an3n �� ������{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����PAB�͵���ABCD����PABΪ�������Σ�AB��AD��CD��AD����E��MΪ�߶�BC��AD���е㣬F��G�ֱ�Ϊ�߶�PA��AE��һ�㣬��AB=AD=2��PF=2FA�� 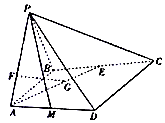
��1��ȷ����G��λ�ã�ʹ��FG��ƽ��PCD��
��2�����ʣ�ֱ��CD���Ƿ����һ��Q��ʹ��ƽ��PAB��ƽ��PMQ���������ǵĴ�СΪ30�㣬�����ڣ���DQ�ij����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������ԭ�㣬����
��������ԭ�㣬����![]() ��
��![]() ��
��![]() ���ϣ�������Ϊ
���ϣ�������Ϊ![]() ������Բ
������Բ![]() ����һ����
����һ����![]() ��
��![]() ��
��![]() �ľ���֮��Ϊ4��
�ľ���֮��Ϊ4��
(��) ����ԲE�ķ��̣�
(��) ��![]() ��
��![]() ��һ��ƽ���ı��Σ�ʹ����
��һ��ƽ���ı��Σ�ʹ����![]() ��
��![]() ��
��![]() ��
��![]() ������Բ
������Բ![]() �ϣ���ͼ��ʾ.�ж��ı���
�ϣ���ͼ��ʾ.�ж��ı���![]() �ܷ�Ϊ���Σ���˵������.
�ܷ�Ϊ���Σ���˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=xex��ae2x��a��R��ǡ��������ֵ��x1 �� x2��x1��x2������ʵ��a��ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ����������֪ʶ���ٰ���һ�Ρ�����֪ʶ֪���١����ʾ�������һ�˴�һ��).�ִӻ��յ�������2060����ʾ��������ȡ��100�ݣ� ͳ�ƽ���������ͼ����ʾ.
���� ���� | ��ȡ�� �� | ���ȫ�������� | ���ȫ��������ռ����ĸ��� |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
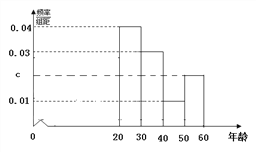
��1���ֱ����n�� a�� b�� c��ֵ��
��2����������[40,60]���ȫ�������������ȡ2�����衰����֮�ǡ�����������[50,60] ������������1�˱����衰����֮�ǡ��ĸ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com