【题目】袋子中有大小、形状完全相同的四个小球，分别写有“和”、“谐”、“校”、“园”四个字，有放回地从中任意摸出一个小球，直到“和”、“谐”两个字都摸到就停止摸球，用随机模拟的方法估计恰好在第三次停止摸球的概率。利用电脑随机产生
到
之间取整数值的随机数，分别用，
，
，代表“和”、“谐”、“校”、“园”这四个字，以每三个随机数为一组，表示摸球三次的结果，经随机模拟产生了以下
组随机数：
由此可以估计，恰好第三次就停止摸球的概率为（ ）
A. 
B. 
C. 
D. 
科目：高中数学 来源： 题型：
【题目】为响应“文化强国建设”号召，并增加学生们对古典文学的学习兴趣，雅礼中学计划建设一个古典文学熏陶室.为了解学生阅读需求，随机抽取200名学生做统计调查.统计显示，男生喜欢阅读古典文学的有64人，不喜欢的有56人；女生喜欢阅读古典文学的有36人，不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系？
(2)为引导学生积极参与阅读古典文学书籍，语文教研组计划牵头举办雅礼教育集团古典文学阅读交流会.经过综合考虑与对比，语文教研组已经从这200人中筛选出了5名男生代表和4名女生代表，其中有3名男生代表和2名女生代表喜欢古典文学.现从这9名代表中任选3名男生代表和2名女生代表参加交流会，记
为参加交流会的5人中喜欢古典文学的人数，求的分布列及数学期望
.
附：
，其中
.
参考数据：
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-5：不等式选讲
已知f（x）＝|x+a|（a∈R）．
（1）若f（x）≥|2x﹣1|的解集为[0，2]，求a的值；
（2）若对任意x∈R，不等式f（x）+|x﹣a|≥3a﹣2恒成立，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某餐厅通过查阅了最近5次食品交易会参会人数
(万人)与餐厅所用原材料数量
(袋)，得到如下统计表：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
（1）根据所给5组数据，求出
关于
的线性回归方程
.
（2）已知购买原材料的费用
(元)与数量
(袋)的关系为
，
投入使用的每袋原材料相应的销售收入为700元，多余的原材料只能无偿返还，据悉本次交易大会大约有15万人参加，根据(1)中求出的线性回归方程，预测餐厅应购买多少袋原材料，才能获得最大利润，最大利润是多少？(注：利润
销售收入
原材料费用).
参考公式： 
， 
.
参考数据： 
， 
， 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于数列
，若存在常数M>0，对任意的n∈N*，恒有
，则称数列为B-数列.
(1)首项为1，公比q(
)的等比数列是否为B-数列？请说明理由；
(2)设Sn是数列{xn}的前n项和，给出下列两组论断：
A组：①数列{xn}是B-数列，②数列{xn}不是B-数列
B组：①数列{Sn}是B-数列，②数列{Sn}不是B-数列
请以其中一组的一个论断为条件，另一组的一个论断为结论组成一个命题.判断所给命题的真假，并证明你的结论.
(3)若数列{an}、
都是B-数列，证明：数列{anbn}也是B-数列
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校2011年到2019年参加“北约”“华约”考试而获得加分的学生人数（每位学生只能参加“北约”“华约”中的一种考试）可以通过以下表格反映出来．（为了方便计算，将2011年编号为1，2012年编号为2，依此类推）
年份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数y | 2 | 3 | 5 | 4 | 5 | 7 | 8 | 10 | 10 |
（1）求这九年来，该校参加“北约”“华约”考试而获得加分的学生人数的平均数和方差；
（2）根据最近五年的数据，利用最小二乘法求出y与x的线性回归方程，并依此预测该校2020年参加“北约”“华约”考试而获得加分的学生人数．（最终结果精确至个位）
参考数据：回归直线的方程是
，其中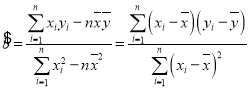
，
．
，
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，直线
的参数方程为
（
为参数），直线
与直线平行，且过坐标原点，圆
的参数方程为
（
为参数）．以坐标原点为极点，
轴的正半轴为极轴建立极坐标系．
（1）求直线和圆的极坐标方程；
（2）设直线和圆相交于点
、
两点，求
的周长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
