
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,
,![]()
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,是否存在q的某些取值,使数列
,是否存在q的某些取值,使数列![]() 中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由.
中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由.
(3)若![]() ,是否存在
,是否存在![]() ,使数列
,使数列![]() 中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由.
中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由.
科目:高中数学 来源: 题型:
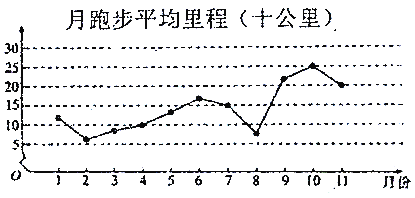
【题目】微信运动,是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注微信运动公众号查看自己每天或每月行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
根据折线图,下列结论正确的是( )
A. 月跑步平均里程的中位数为![]() 月份对应的里程数
月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在![]() 、
、![]() 月
月
D. ![]() 月至
月至![]() 月的月跑步平均里程相对于
月的月跑步平均里程相对于![]() 月至
月至![]() 月,波动性更小,变化比较平稳
月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下面四个命题:
①“若![]() ,则
,则![]() 或
或![]() ”的逆否命题为“若
”的逆否命题为“若![]() 且
且![]() ,则
,则![]() ”
”
②命题:“![]() ,若
,若![]() ,则
,则![]() ”,用反证法证明时应假设
”,用反证法证明时应假设![]() 或
或![]() .
.
③命题![]() 存在
存在![]() ,使得
,使得![]() ,则
,则![]() :任意
:任意![]() ,都有
,都有![]()
④若![]() 且
且![]() 为假命题,则
为假命题,则![]() 均为假命题,其中真命题个数为( )
均为假命题,其中真命题个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的普通方程为
的普通方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),其中
为参数),其中![]() .以坐标
.以坐标![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴,建立极坐标系.
轴非负半轴为极轴,建立极坐标系.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ,
,![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 的交点分别为
的交点分别为![]() ,
,![]() .当
.当![]() 为等腰直角三角形时,求直线
为等腰直角三角形时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的方程为
的方程为![]() ,以极点为原点,极轴所在直线为
,以极点为原点,极轴所在直线为![]() 轴建立直角坐标,直线
轴建立直角坐标,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ;若
;若![]() 、
、![]() 、
、![]() 成等比数列,求
成等比数列,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() :
:![]() 上的一点,其焦点为点
上的一点,其焦点为点![]() ,且抛物线
,且抛物线![]() 在点
在点![]() 处的切线
处的切线![]() 交圆
交圆![]() :
:![]() 于不同的两点
于不同的两点![]() ,
,![]() .
.
(1)若点![]() ,求
,求![]() 的值;
的值;
(2)设点![]() 为弦
为弦![]() 的中点,焦点
的中点,焦点![]() 关于圆心
关于圆心![]() 的对称点为
的对称点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当x∈[0,π]时,f(x)≥0恒成立,求实数a的取值范围;(参考数据:sin1≈0.84)
(2)当a=1时,数列{an}满足:0<an<1,![]() =f(an),求证:{an}是递减数列.
=f(an),求证:{an}是递减数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后得到如图的频率分
后得到如图的频率分
布直方图.

(1)求图中实数![]() 的值;
的值;
(2)若该校高一年级共有学生1000人,试估计该校高一年级期中考试数学成绩不低于60分的人数.
(3)若从样本中数学成绩在![]() ,
,![]() 与
与![]() ,
,![]() 两个分数段内的学生中随机选取2名学生,试用列举法求这2名学生的数学成绩之差的绝对值大于10的槪率.
两个分数段内的学生中随机选取2名学生,试用列举法求这2名学生的数学成绩之差的绝对值大于10的槪率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com