
【题目】已知直三棱柱![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,且
,且![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.
的中点.
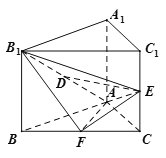
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1) 根据直线与平面平行的判定定理可知,只要在平面ABC里面找到一条直线与DE平行即可,过DE构造平行四边形,使其与平面ABC相交,则可得DE与交线平行,所以进一步可得DE∥平面ABC;
(2) 以点A为坐标原点,如图建立空间直角坐标系O﹣xyz,求出直线![]() 的方向向量,平面
的方向向量,平面![]() 的法向量,代入公式,即可得到结果.
的法向量,代入公式,即可得到结果.
(1)设AB的中点为G,连接DG,CG,则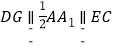 ,
,
四边形DGCE为平行四边形,∴DE∥GC,又DEABC,GCABC∴DE∥平面ABC.
(2)以点A为坐标原点,![]() 的方向为
的方向为![]() 轴的正方向建立空间直角坐标系,
轴的正方向建立空间直角坐标系,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,
,
则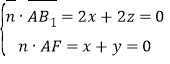 ,令
,令![]() ,则
,则![]() .
.
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
所以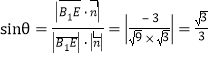


科目:高中数学 来源: 题型:
【题目】某二手交易市场对某型号的二手汽车的使用年数![]() (
(![]() )与销售价格
)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
(I)试求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() .
.
(参考公式: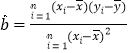 ,
,![]() )
)
(II)已知每辆该型号汽车的收购价格为![]() 万元,根据(I)中所求的回归方程,预测
万元,根据(I)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?(利润=销售价格-收购价格)
最大?(利润=销售价格-收购价格)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4男3女站成一排,求满足下列条件的排法共有多少种?
![]() 任何两名女生都不相邻,有多少种排法?
任何两名女生都不相邻,有多少种排法?
![]() 男甲不在首位,男乙不在末位,有多少种排法?
男甲不在首位,男乙不在末位,有多少种排法?
![]() 男生甲、乙、丙顺序一定,有多少种排法?
男生甲、乙、丙顺序一定,有多少种排法?
![]() 男甲在男乙的左边
男甲在男乙的左边![]() 不一定相邻
不一定相邻![]() 有多少种不同的排法?
有多少种不同的排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,一个长轴端点为![]() ,离心率
,离心率![]() ,过P分别作斜率为
,过P分别作斜率为![]() 的直线PA,PB,交椭圆于点A,B。
的直线PA,PB,交椭圆于点A,B。
(1)求椭圆的方程;
(2)若![]() ,则直线AB是否经过某一定点?
,则直线AB是否经过某一定点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·吉林期末]一个袋中装有6个大小形状完全相同的球,球的编号分别为1,2,3,4,5,6.
(1)从袋中随机抽取两个球,求取出的球的编号之和为6的概率;
(2)先后有放回地随机抽取两个球,两次取的球的编号分别记为![]() 和
和![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a3=7,a5+a7=26,{an}的前n项和为Sn.
(1)求an及Sn;
(2)令bn=![]() (n∈N*),求数列{bn}的前n项和Tn.
(n∈N*),求数列{bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com