Question

12£®ÒÑÖªÍÖÔ²${C_1}£º\frac{x^2}{a^2}+\frac{y^2}{b^2}=1£¨a£¾b£¾0£©$µÄ×óÓÒ½¹µã·Ö±ðΪF₁£¬F₂£¬ÇÒF₂ΪÅ×ÎïÏß${C_2}£º{y^2}=2px$µÄ½¹µã£¬C₂µÄ×¼Ïßl±»C₁ºÍÔ²x²+y²=a²½ØµÃµÄÏÒ³¤·Ö±ðΪ$2\sqrt{2}$ºÍ4£®
£¨1£©ÇóC₁ºÍC₂µÄ·½³Ì£»
£¨2£©Ö±Ïßl₁¹ýF₁ÇÒÓëC₂²»Ïཻ£¬Ö±Ïßl₂¹ýF₂ÇÒÓël₁ƽÐУ¬Èôl₁½»C₁ÓÚA£¬B£¬l₂½»C₁½»ÓÚC£¬D£¬ÇÒÔÚxÖáÉÏ·½£¬ÇóËıßÐÎAF₁F₂CµÄÃæ»ýµÄÈ¡Öµ·¶Î§£®

Answer 1

·ÖÎö £¨1£©ÓÉÍÖÔ²¼°Å×ÎïÏßµÄÐÔÖÊ£¬Áз½³Ì×éÇóµÃa£¬bºÍcµÄÖµ£¬¼´¿ÉÇóµÃC₁ºÍC₂µÄ·½³Ì£»
£¨2£©ÉèÖ±Ïß·½³Ì£¬´úÈëÅ×ÎïÏߺÍÍÖÔ²·½³Ì£¬ÇóµÃØ­ABØ­£¬ÔòABÓëCD¼äµÄ¾àÀëΪ$\frac{4}{{\sqrt{{t^2}+1}}}$£¬ÀûÓÃÍÖÔ²µÄ¶Ô³ÆÐÔ¼°º¯Êýµ¥µ÷ÐÔ¼´¿ÉÇóµÃËıßÐÎAF₁F₂CµÄÃæ»ýµÄÈ¡Öµ·¶Î§£®

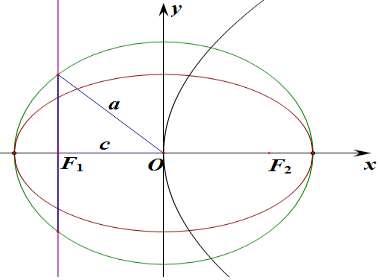½â´ð ½â£º£¨1£©ÓÉÌâÒâ¿ÉÖª£ºÅ×ÎïÏßµÄ×¼Ïß·½³Ìx=-$\frac{p}{2}$£¬c=$\frac{p}{2}$£¬
C₂µÄ×¼Ïßl±»C₁ºÍÔ²x²+y²=a²½ØµÃµÄÏÒ³¤·Ö±ðΪ$2\sqrt{2}$ºÍ4£¬
$\left\{\begin{array}{l}\frac{{2{b^2}}}{a}=2\sqrt{2}\\ 2b=4\end{array}\right.$£¬µÃ$a=2\sqrt{2}£¬b=c=2£¬p=4$£¬
¡àC₁ºÍC₂µÄ·½³Ì·Ö±ðΪ$\frac{x^2}{8}+\frac{y^2}{4}=1£¬{y^2}=8x$£®
£¨2£©ÓÉÌâÒ⣬ABµÄбÂʲ»Îª0£¬ÉèAB£ºx=ty-2£¬
ÓÉ$\left\{\begin{array}{l}x=ty-2\\{y^2}=8x\end{array}\right.$£¬µÃy²-8ty+16=0£¬¡÷=64t²-64¡Ü0£¬µÃt²¡Ü1£¬
ÓÉ$\left\{\begin{array}{l}x=ty-2\\{x^2}+2{y^2}-8=0\end{array}\right.$£¬µÃ£¨t²+1£©y²-4ty-4=0£¬
$|{AB}|=2a+e£¨{x_1}+{x_2}£©=\frac{{\sqrt{2}}}{2}t£¨{y_1}+{y_2}£©+2\sqrt{2}=\frac{{4\sqrt{2}£¨{t^2}+1£©}}{{{t^2}+2}}$£¬ABÓëCD¼äµÄ¾àÀëΪ$\frac{4}{{\sqrt{{t^2}+1}}}$£¬
ÓÉÍÖÔ²µÄ¶Ô³ÆÐÔ£¬ABDCΪƽÐÐËıßÐΣ¬${S_{¡÷{F_1}{F_2}C}}=\frac{1}{2}{S_{ABDC}}=\frac{1}{2}•\frac{{4\sqrt{2}£¨{t^2}+1£©}}{{{t^2}+2}}•\frac{4}{{\sqrt{{t^2}+1}}}=\frac{{8\sqrt{2}\sqrt{{t^2}+1}}}{{{t^2}+2}}$£¬
Éè$\sqrt{{t^2}+1}=m£¬m¡Ê[{1£¬\sqrt{2}}]$£¬
${S_{A{F_1}{F_2}C}}=\frac{{8\sqrt{2}}}{{m+\frac{1}{m}}}¡Ê[\frac{16}{3}£¬4\sqrt{2}]$£®
¼´ÎªËıßÐÎAF₁F₂CµÄÃæ»ýµÄÈ¡Öµ·¶Î§£®

µãÆÀ ±¾Ì⿼²éÍÖÔ²¼°Å×ÎïÏߵķ½³Ì¼°¼òµ¥¼¸ºÎÐÔÖÊ£¬¿¼²éÖ±ÏßÓëÍÖÔ²µÄλÖùØϵ£¬¿¼²éΤ´ï¶¨Àí£¬ÏÒ³¤¹«Ê½£¬Èý½ÇÐεÄÃæ»ý¹«Ê½£¬¿¼²é¼ÆËãÄÜÁ¦£¬ÊôÓÚÖеµÌ⣮