
科目:高中数学 来源: 题型:
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| c |
| e1 |
| e2 |
| b |
| c |
| a |
| a |
| b |
| c |
| a |
| c |
| b |
| a |
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学必修4 2.3向量的坐标表示练习卷(解析版) 题型:选择题
已知向量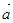 =(-2,4),
=(-2,4), =(1,-2),则
=(1,-2),则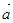 与
与 的关系是
(
)
的关系是
(
)
A.不共线 B.相等 C.同向 D.反向
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省保定市八校联合体高一(上)期末数学试卷(解析版) 题型:解答题
 为两个不共线的向量,
为两个不共线的向量,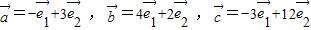 ,试用
,试用 为基底表示向量
为基底表示向量 ;
; ,当k为何值时,
,当k为何值时, ∥
∥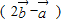 ?平行时它们是同向还是反向?
?平行时它们是同向还是反向?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com