
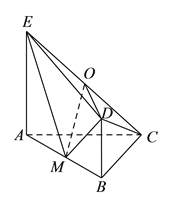
【题目】如图,平面![]() 平面
平面![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,四边形
,四边形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
(I)求证:![]() 平面
平面![]() .
.
(II)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
(III)能否在![]() 上找一点
上找一点![]() ,使得
,使得![]() 平面
平面![]() ?若能,请指出点
?若能,请指出点![]() 的位置,并加以证明;若不能,请说明理由.
的位置,并加以证明;若不能,请说明理由.
【答案】(I)见解析;(II)![]() ;(III)见解析.
;(III)见解析.
【解析】试题分析:(1)先建立空间直角坐标系,利用法向量证明OD//平面ABC,说明![]() 和平面ABC的法向量
和平面ABC的法向量![]() 垂直即可;(2)设直线CD与平面ODM所成角为θ,求出平面ODM法向量
垂直即可;(2)设直线CD与平面ODM所成角为θ,求出平面ODM法向量![]() ,则
,则 ;(3)设EM上一点N满足,
;(3)设EM上一点N满足,![]() 平面ABDE法向量
平面ABDE法向量![]() ,
,![]() 不存在
不存在![]() 使
使![]() ∴ 不存在满足题意的点N.
∴ 不存在满足题意的点N.
试题解析:以B为原点,BC为x轴,BA为y轴,BD为z轴,建立空间直角坐标系
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)平面ABC的法向量![]() ,
,![]() ,
,![]()
∴OD//平面ABC
(2)设平面ODM法向量为![]() ,直线CD与平面ODM所成角为θ
,直线CD与平面ODM所成角为θ
![]() ,
,![]() ,∴
,∴![]() ,
,![]()
∴ .
.
(3)设EM上一点N满足,![]()
平面ABDE法向量![]() ,
,![]()
不存在![]() 使
使![]() ∴不存在满足题意的点N.
∴不存在满足题意的点N.
(传统方法参照给分)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )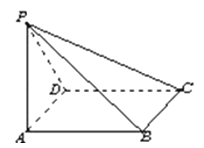
A.在棱AD上存在点M,使AD⊥平面PMB
B.异面直线AD与PB所成的角为90°
C.二面角P﹣BC﹣A的大小为45°
D.BD⊥平面PAC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知圆![]() 的圆心在直线
的圆心在直线![]() 上,且过点
上,且过点![]() ,与直线
,与直线![]() 相切.
相切.
(![]() )求圆
)求圆![]() 的方程.
的方程.
(![]() )设直线
)设直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点.求实数
两点.求实数![]() 的取值范围.
的取值范围.
(![]() )在(
)在(![]() )的条件下,是否存在实数
)的条件下,是否存在实数![]() ,使得弦
,使得弦![]() 的垂直平分线
的垂直平分线![]() 过点
过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一枚质地均匀且四个面上分别标有1,2,3,4的正四面体先后抛掷两次,其底面落于桌面上,记第一次朝下面的数字为![]() ,第二次朝下面的数字为
,第二次朝下面的数字为![]() .用
.用![]() 表示一个基本事件.
表示一个基本事件.
请写出所有基本事件;
求满足条件“![]() ”为整数的事件的概率;
”为整数的事件的概率;
求满足条件“![]() ”的事件的概率.
”的事件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com