(-9,-3]
分析:由题意可得函数在[0,3]上单调递增,再由偶函数的图象关于y轴(x=0)对称,故在[-3,0]上为减函数.令x=-3求得f(3)=0,f(x+6)=f(x),f(x)是周期等于6的周期函数,故函数关于x=6对称,求得f(-9)=0,f(-3)=0,f(3)=0=f(6)=f(9),要使方程f(x)=0在区间[a,6-a]上恰有3个不同实根,则区间长度6-2a 满足 12≤6-2a<15,
由此求得实数a的取值范围.
解答:∵当x
1,x
2∈[0,3]且x
1≠x
2时,都有
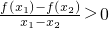
,可知函数在[0,3]上单调递增.
又f(x)为偶函数,图象关于y轴(x=0)对称,故在[-3,0]上为减函数.
令x=-3,则由f(x+6)=f(x)+f(3)得f(3)=f(-3)+f(3)=2f(3),故f(3)=0
因为f(x+6)=f(x)+f(3)=f(x)+0=f(x),所以f(x)是周期等于6的周期函数,故函数关于x=6对称,
所以f(9)=0,
因为y=f(x)是R上的偶函数,f(-9)=0,f(-3)=0,
因为f(x)在[0,3]上是增函数,所以[0,3]上只有一解为3,对称性[-3,0]只有一解为-3,
因为f(x+6)=f(x)+f(3),且f(x)在[0,3]上是增函数,
所以f(x)在[6,9]上是增函数,所以[6,9]上只有一解为9,因为f(x)关于x=6对称,
所以f(x)在[3,6]上只有一解为3,
由对称性知[-9,-6],[-6,-3]各只有一解-9,-3,
要使方程f(x)=0在区间[a,6-a]上恰有3个不同实根,则区间长度6-2a 满足 12≤6-2a<15,解得-9<a≤-3.
∴实数a的取值范围是(-9,-3],
故答案为(-9,-3].
点评:本题是一道抽象函数问题,题目的设计“小而巧”,解题的关键是巧妙的赋值,利用其奇偶性和所给的关系式得到函数的周期性,再利用周期性求函数值.灵活的“赋值法”是解决抽象函数问题的基本方法,属于中档题.

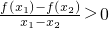 .
.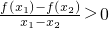 ,可知函数在[0,3]上单调递增.
,可知函数在[0,3]上单调递增.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案