
| |||||||||||||||
(1) |
解:∵f(x)在[-1,0]上是减函数,在[0,2]上是增函数 ∴x=0点是f(x)的一个极值点 ∴ 即x=0是3ax2+2x+c=0的一个根 ∴c=0 分析:(1)由f(x)在[-1,0]上递减,在[0,2]上递增,可得x=0是f(x)的一个极值点,便可求出c的值. |
(2) |
解:∵f(x)在[-1,0]上是减函数,在[0,2]上是增函数, ∴x=0点是f(x)的一个极值点, ∴ 即x=0是3ax2+2x+c=0的一个根. ∴c=0. ∵函数f(x)的图象过点(2,0),∴f(2)=0. ∴8a+4+d=0,即d=-8a-4. 令 ∴x1=0,x2=- ∵f(x)在[0,2]上为增函数,在[4,5]上为减函数,∴x2∈[2,4], 即 ∴-6≤ 即- ∴- 即- 分析:由f(x)在[0,2]上递增,在[4,5]上递减,可得函数的另一个极值点在[2,4]上,这样就可建立相应的不等式求出d的取值范围. |
(3) |
解:假设存在点M(x0,y0),使得曲线y=f(x)在点M处的切线的斜率为3,则 即3a ∴3a 又- ∴△=4+36a<0. ∴不存在点M(x0,y0),使得曲线y=(x)在点M处的切线的斜率为3. 分析:求得f(x)在x=x0时的导数,并使其为3,这样可以建立关于x0的方程,通过判别式判断有无实根就可以确定点M是否存在. |


科目:高中数学 来源:2009年高考数学第二轮复习热点专题测试:不等式(含详解) 题型:013
已知函数:f(x)=x2+bx=c,其中:0≤b≤4,0≤c≤4,记函数f(x)满足条件:![]() 的事件为A,则事件A发生的概率为
的事件为A,则事件A发生的概率为
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源:山东省潍坊市2012届高三一轮模拟考试数学理科试题 题型:013
若直角坐标平面内的两点P、Q满足条件:
①P、Q都在函数y=f(x)的图象上;
②P、Q关于原点对称.
则称点对[P,Q]是函数Y=f(x)的一对“友好点对”(点对[P,Q]与[Q,P]看作同一对“友好点对”).已知函数,f(x)=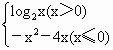 ,则此函数的“友好点对”有
,则此函数的“友好点对”有
A.0对
B.1对
C.2对
D.3对
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三8月月考理科数学试卷(解析版) 题型:解答题
已知函数 f(x)=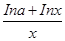 在[1,+∞)上为减函数,求实数a的取值范围.
在[1,+∞)上为减函数,求实数a的取值范围.
【解析】本试题考查了导数在研究函数中的运用。根据函数f(x)=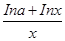 在[1,+∞)上为减函数,可知导函数在给定区间恒小于等于零,f ′(x)≤0在[1,+∞)上恒成立,lna≥1-lnx在[1,+∞)上恒成立.然后利用φ(x)=1-lnx,φ(x)max=1,从而得到a≥e
在[1,+∞)上为减函数,可知导函数在给定区间恒小于等于零,f ′(x)≤0在[1,+∞)上恒成立,lna≥1-lnx在[1,+∞)上恒成立.然后利用φ(x)=1-lnx,φ(x)max=1,从而得到a≥e
f ′(x)=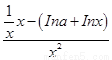 =
=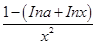 ,因为 f(x)在[1,+∞)上为减函数,故 f ′(x)≤0在[1,+∞)上恒成立,即lna≥1-lnx在[1,+∞)上恒成立.设φ(x)=1-lnx,φ(x)max=1,故lna≥1,a≥e,
,因为 f(x)在[1,+∞)上为减函数,故 f ′(x)≤0在[1,+∞)上恒成立,即lna≥1-lnx在[1,+∞)上恒成立.设φ(x)=1-lnx,φ(x)max=1,故lna≥1,a≥e,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com