
(本小题满分12分)
函数f(x)=  sinωxcosωx+sin2ωx+
sinωxcosωx+sin2ωx+ ,其图像相邻两条对称轴之间的距离为
,其图像相邻两条对称轴之间的距离为 .
.
(Ⅰ)求ω的值;
(Ⅱ) 若A为△ABC的内角,且f =
= ,求A的值.
,求A的值.
(Ⅰ)f(x)= sin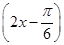 +1;(2)A=
+1;(2)A= 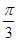 .
.
解析试题分析:(1)将f(x)解析式第一项利用二倍角的余弦函数公式化简,第二项第二个因式利用诱导公式变形,再利用二倍角的正弦函数公式化简,整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数,由y=f(x)的图象相邻两条对称轴之间的距离为  ,得到f(x)的周期为π,利用周期公式求出ω的值.确定出f(x)的解析式.
,得到f(x)的周期为π,利用周期公式求出ω的值.确定出f(x)的解析式.
(2)由f =sin
=sin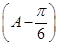 +1=
+1= ∴sin
∴sin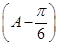 =
= ,再结合A∈(0,π),可得A=
,再结合A∈(0,π),可得A= 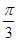 .
.
(Ⅰ)f(x)=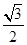 sin2ωx+
sin2ωx+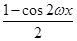 +
+
=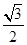 sin2ωx?
sin2ωx? cos2ωx+1=sin
cos2ωx+1=sin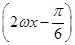 +1
+1
∵函数图像的相邻两条对称轴之间的距离为 ,∴最小正周期T=π
,∴最小正周期T=π
∴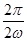 =π,ω=1.
=π,ω=1.
∴f(x)= sin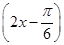 +1
+1
(2) ∵f =sin
=sin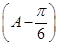 +1=
+1= ∴sin
∴sin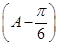 =
=
∵ A∈(0,π) ∴ ?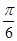 < A?
< A?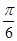 <
< 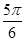
∴ A?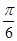 =
= 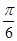 ,故A=
,故A= 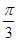 .
.
考点:考查了三角诱导公式及三角函数的图像及性质,给值求角等知识.
点评:掌握三角诱导公式是化简的基础,再求解的过程中要注意角的范围,本小题同时还考查了三角函数的图像及三角函数的性质,属于容易题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本题满分14分)已知函数 (其中
(其中 )的图象与
)的图象与 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为 ,且图象上一个点为
,且图象上一个点为 .
.
(1)求 的解析式;
的解析式;
(2)若 求函数
求函数 的值域;
的值域;
(3)将函数 的图象向左平移
的图象向左平移 个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,求经以上变换后得到的函数解析式.
个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,求经以上变换后得到的函数解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (
( )的部分图像,
)的部分图像,  是这部分图象与
是这部分图象与 轴的交点(按图所示),函数图象上的点
轴的交点(按图所示),函数图象上的点 满足:
满足: .
.
(Ⅰ)求函数 的周期;
的周期;
(Ⅱ)若 的横坐标为1,试求函数
的横坐标为1,试求函数 的解析式,并求
的解析式,并求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com