
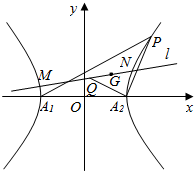
 已知中心在原点,左、右顶点A1、A2在x轴上,离心率为$\frac{\sqrt{21}}{3}$的双曲线C经过点P(6,6),动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N,Q为线段MN的中点.
已知中心在原点,左、右顶点A1、A2在x轴上,离心率为$\frac{\sqrt{21}}{3}$的双曲线C经过点P(6,6),动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N,Q为线段MN的中点.分析 (1)根据题意,双曲线的离心率e=$\frac{\sqrt{21}}{3}$,由双曲线的性质,可得$\frac{{b}^{2}}{{a}^{2}}$=$\frac{12}{9}$,进而可将双曲线方程为$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{12}$=λ,λ≠0;将P的坐标代入,可得λ的值,进而可得答案;
(2)首先根据P、A1、A2的坐标得到三角形重心G的坐标,再假设存在直线l,使G(2,2)平分线段MN,设出M、N的坐标,分别为(x1,y1),(x2,y2),则l的方程可以设为y=m(x-2)+2,与双曲线方程联立消去y,可得关于x的一元二次方程,利用$\overrightarrow{Q{A}_{2}}$•$\overrightarrow{P{A}_{2}}$=0,可得(3-x,-y)•(-3,-6)=0,可得答案.
解答 解:(1)根据题意,双曲线的离心率e=$\frac{\sqrt{21}}{3}$,
则$\frac{{c}^{2}}{{a}^{2}}$=$\frac{21}{9}$,可得$\frac{{b}^{2}}{{a}^{2}}$=$\frac{12}{9}$.
设双曲线方程为$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{12}$=λ,λ≠0;
由已知,双曲线过点P(6,6),
将其坐标代入方程,解可得λ=1,
所以所求双曲线方程为$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{12}$=1;
(2)P、A1、A2的坐标依次为(6,6)、(-3,0)、(3,0),
∴三角形的重心G的坐标为(2,2)
设M(x1,y1),N(x2,y2),Q(x,y).
∴l的方程为y=m(x-2)+2,与双曲线方程联立消去y,
整理得(4-3m2)x2+(12m2-12m)x+3(2-2m)2-36=0.
∴x=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{6{m}^{2}-6m}{4-3{m}^{2}}$,y=$\frac{8-8m}{4-3{m}^{2}}$
$\overrightarrow{Q{A}_{2}}$•$\overrightarrow{P{A}_{2}}$=0,可得(3-x,-y)•(-3,-6)=0,
∴x+2y-3=0,
∴-$\frac{6{m}^{2}-6m}{4-3{m}^{2}}$+2×$\frac{8-8m}{4-3{m}^{2}}$-3=0
∴m=$\frac{5±\sqrt{13}}{3}$,
∴直线l的斜率为$\frac{5±\sqrt{13}}{3}$时,$\overrightarrow{Q{A}_{2}}$•$\overrightarrow{P{A}_{2}}$=0.
点评 本题考查直线与双曲线的位置关系,计算量比较大,解题时,充分利用题干的条件,简化方程,可以降低运算量,提高准确率.


科目:高中数学 来源: 题型:解答题
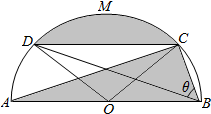 如图:阴影部分是一个机械构件.该构件是由一块半圆形铁皮剪切后,剩下了弓形面CMD,及三角形ABC所形成的.其中半圆直径AB=8,CD∥AB,点M是$\widehat{CD}$上一点,∠CBD=θ.
如图:阴影部分是一个机械构件.该构件是由一块半圆形铁皮剪切后,剩下了弓形面CMD,及三角形ABC所形成的.其中半圆直径AB=8,CD∥AB,点M是$\widehat{CD}$上一点,∠CBD=θ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}\;km$ | B. | $\sqrt{13}\;km$ | C. | $\sqrt{19}\;km$ | D. | $\sqrt{10-3\sqrt{3}}\;km$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
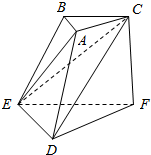 如图,三棱台ABC-DEF中,CF⊥平面DEF,AC⊥BC,且DF=EF=CF=2AC.
如图,三棱台ABC-DEF中,CF⊥平面DEF,AC⊥BC,且DF=EF=CF=2AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
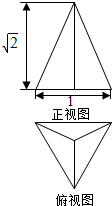 已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{4}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com