
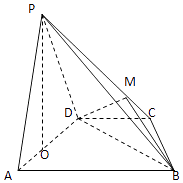
【题目】如图,在四棱锥P﹣ABCD中,AD=4,BD=8,平面PAD⊥平面ABCD,AB=2DC=4 ![]() . (Ⅰ)设M是线段PC上的一点,证明:平面BDM⊥平面PAD
. (Ⅰ)设M是线段PC上的一点,证明:平面BDM⊥平面PAD
(Ⅱ)求四棱锥P﹣ABCD的体积.
【答案】(Ⅰ)证明:在△ABD中,AD=4,BD=8,AB=4 ![]() , ∵AD2+BD2=AB2 ,
, ∵AD2+BD2=AB2 ,
∴∠ADB=90°,即AD⊥BD.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
BD平面ABCD,
∴BD⊥平面PAD,
又BD平面MBD,
∴平面MBD⊥平面PAD.
(Ⅱ)解:过P作PO⊥AD交AD于O,
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
PO平面PAD,
∴PO⊥平面ABCD.
∴线段PO为四棱锥P﹣ABCD的高,
在四边形ABCD中,∵AB∥DC,AB=2DC,
∴四边形ABCD是梯形,在Rt△ADB中,斜边AB边上的高为 ![]() =
= ![]() ,
,
即梯形ABCD的高为 ![]() ,
,
∴梯形ABCD的面积为S= ![]() =24.
=24.
∴VP﹣ABCD= ![]() =16
=16 ![]() .
.
【解析】(Ⅰ)在△ABD中,由AD2+BD2=AB2 , 可得∠ADB=90°.又平面PAD⊥平面ABCD,可得BD⊥平面PAD,夹角证明.(Ⅱ)过P作PO⊥AD交AD于O,利用线面垂直的性质定理可得:PO⊥平面ABCD.即线段PO为四棱锥P﹣ABCD的高,利用梯形的面积计算公式可得梯形ABCD的面积为S.即可得出VP﹣ABCD .
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已成椭圆 ![]() 的离心率为
的离心率为 ![]() .其右顶点与上顶点的距离为
.其右顶点与上顶点的距离为 ![]() ,过点
,过点 ![]() 的直线
的直线 ![]() 与椭圆
与椭圆 ![]() 相交于
相交于 ![]() 两点.
两点.
(1)求椭圆 ![]() 的方程;
的方程;
(2)设 ![]() 是
是 ![]() 中点,且
中点,且 ![]() 点的坐标为
点的坐标为 ![]() ,当
,当 ![]() 时,求直线
时,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l1的方程为y= ![]() x,曲线C的参数方程为
x,曲线C的参数方程为 ![]() (φ是参数,0≤φ≤π).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ是参数,0≤φ≤π).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)分别写出直线l1与曲线C的极坐标方程;
(2)若直线 ![]() =0,直线l1与曲线C的交点为A,直线l1与l2的交点为B,求|AB|.
=0,直线l1与曲线C的交点为A,直线l1与l2的交点为B,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生小王在学习完解三角形的相关知识后,用所学知识测量高为AB 的烟囱的高度.先取与烟囱底部B在同一水平面内的两个观测点C,D,测得∠BDC=60°,∠BCD=75°,CD=40米,并在点C处的正上方E处观测顶部 A的仰角为30°,且CE=1米,则烟囱高 AB=米.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 f (x)=|x﹣1|+|x﹣a|(a∈R).
(1)若a=﹣3,求函数 f (x)的最小值;
(2)如果x∈R,f (x)≤2a+2|x﹣1|,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的最小正周期为π,将函数f(x)的图象向右平移
的最小正周期为π,将函数f(x)的图象向右平移 ![]() 个所得图象对应的函数为y=g(x),则关于函数为y=g(x)的性质,下列说法不正确的是( )
个所得图象对应的函数为y=g(x),则关于函数为y=g(x)的性质,下列说法不正确的是( )
A.g(x)为奇函数
B.关于直线 ![]() 对称
对称
C.关于点(π,0)对称
D.在 ![]() 上递增
上递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,∠CAD=90°,EF∥BC,EF= ![]() BC,AC=
BC,AC= ![]() ,AE=EC=1.
,AE=EC=1. 
(1)求证:CE⊥AF;
(2)若二面角E﹣AC﹣F 的余弦值为 ![]() ,求点D 到平面ACF 的距离.
,求点D 到平面ACF 的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“a≤0”是“函数f(x)=|(ax﹣1)x|在区间(0,+∞)内单调递增”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)在定义域R上的导函数为f′(x),若方程f'(x)=0无解,且f[f(x)﹣2017x]=2017,当g(x)=sinx﹣cosx﹣kx在[﹣ ![]() ,
, ![]() ]上与f(x)在R上的单调性相同时,则实数k的取值范围是( )
]上与f(x)在R上的单调性相同时,则实数k的取值范围是( )
A.(﹣∞,﹣1]
B.(﹣∞, ![]() ]
]
C.[﹣1, ![]() ]
]
D.[ ![]() ,+∞)
,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com