
已知直线l:y=x+m,m∈R.
(1)若以点M(2,0)为圆心的圆与直线l相切于点P,且点P在y轴上,求该圆的方程;
(2)若直线l关于x轴对称的直线为l′,问直线l′与抛物线C:x2=4y是否相切?说明理由.
(1)(x-2)2+y2=8.(2)当m=1时,直线l′与抛物线C相切.
当m≠1时,直线l′与抛物线C不相切
【解析】法一:(1)依题意,点P的坐标为(0,m).
因为MP⊥l,
所以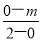 ×1=-1,
×1=-1,
解得m=2,即点P的坐标为(0,2).
从而圆的半径r=|MP|=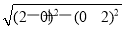 =2
=2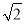 .?
.?
故所求圆的方程为(x-2)2+y2=8.
(2)因为直线l的方程为y=x+m,
所以直线l′的方程为y=-x-m.
由 得x2+4x+4m=0.
得x2+4x+4m=0.
Δ=42-4×4m=16(1-m).
①当m=1,即Δ=0时,直线l′与抛物线C相切;
②当m≠1,即Δ≠0时,直线l′与抛物线C不相切.
综上,
.
法二(1)设所求圆的半径为r,
则圆的方程可设为(x-2)2+y2=r2.
依题意,所求圆与直线l:x-y+m=0相切于点P(0,m),
则 解得
解得
所以所求圆的方程为(x-2)2+y2=8.
(2)同法一.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-2练习卷(解析版) 题型:解答题
设矩阵M=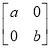 (其中a>0,b>0).
(其中a>0,b>0).
(1)若a=2,b=3,求矩阵M的逆矩阵M-1;
(2)若曲线C:x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C′: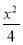 +y2=1,求a,b的值.
+y2=1,求a,b的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-1练习卷(解析版) 题型:填空题
用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有________个.(用数字作答)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-3练习卷(解析版) 题型:选择题
若双曲线 =1(a>0,b>0)与直线y=
=1(a>0,b>0)与直线y= x无交点,则离心率e的取值范围是( ).
x无交点,则离心率e的取值范围是( ).
A.(1,2) B.(1,2] C.(1, ) D.(1,
) D.(1, ]
]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-2练习卷(解析版) 题型:选择题
抛物线C1:y= x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2: -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-1练习卷(解析版) 题型:填空题
直线y=2x+3被圆x2+y2-6x-8y=0所截得的弦长等于________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(解析版) 题型:解答题
已知四边形ABCD是菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,G,H分别是CE,CF的中点.

(1)求证:平面AEF∥平面BDGH
(2)若平面BDGH与平面ABCD所成的角为60°,求直线CF与平面BDGH所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(解析版) 题型:选择题
如图所示,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是 ( ).

A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-3-2练习卷(解析版) 题型:填空题
已知△ABC的三边长成公比为 的等比数列,则其最大角的余弦值为________.
的等比数列,则其最大角的余弦值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com