
【题目】已知函数f(x)=cosx(sinx+cosx)﹣![]() .
.
(1)若0<α<![]() , 且sinα=
, 且sinα=![]() , 求f(α)的值;
, 求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
【答案】解:(1)∵0<α<![]() ,且sinα=
,且sinα=![]() ,
,
∴cosα=![]() ,
,
∴f(α)=cosα(sinα+cosα)﹣![]() ,
,
=![]() ×(
×(![]() +)﹣
+)﹣![]()
=![]() .
.
(2)f(x)=cosx(sinx+cosx)﹣![]() .
.
=sinxcosx+cos2x﹣![]()
=![]() sin2x+
sin2x+![]() cos2x
cos2x
=![]() sin(2x+
sin(2x+![]() ),
),
∴T=![]() =π,
=π,
由2kπ﹣![]() ≤2x+
≤2x+![]() ≤2kπ+
≤2kπ+![]() ,k∈Z,得kπ﹣
,k∈Z,得kπ﹣![]() ≤x≤kπ+
≤x≤kπ+![]() ,k∈Z,
,k∈Z,
∴f(x)的单调递增区间为[kπ﹣![]() ,kπ+
,kπ+![]() ],k∈Z.
],k∈Z.
【解析】(1)利用同角三角函数关系求得cosα的值,分别代入函数解析式即可求得f(α)的值.
(2)利用两角和公式和二倍角公式对函数解析式进行恒等变换,进而利用三角函数性质和周期公式求得函数最小正周期和单调增区间.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合.直线l的参数方程为: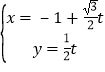 (t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(Ⅰ)写出C的直角坐标方程,并指出C是什么曲线;
(Ⅱ)设直线l与曲线C相交于P、Q两点,求|PQ|值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}前n项和Sn满足Sn+1=a2Sn+a1 , 其中a2≠0.
(Ⅰ)求证数列{an}是首项为1的等比数列;
(Ⅱ)当a2=2时,是否存在等差数列{bn},使得a1bn+a2bn﹣1+a3bn﹣2+…+anb1=2n+1﹣n﹣2对一切n∈N*都成立?若存在,求出bn;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是海面上一条南北方向的海防警戒线,在
是海面上一条南北方向的海防警戒线,在 ![]() 上点
上点 ![]() 处有一个水声监测点,另两个监测点
处有一个水声监测点,另两个监测点 ![]() 分别在
分别在 ![]() 的正东方向
的正东方向 ![]() 处和
处和 ![]() 处.某时刻,监测点
处.某时刻,监测点 ![]() 收到发自目标
收到发自目标 ![]() 的一个声波,
的一个声波,![]() 后监测点
后监测点 ![]() 后监测点
后监测点 ![]() 相继收到这一信号,在当时的气象条件下,声波在水中的传播速度是
相继收到这一信号,在当时的气象条件下,声波在水中的传播速度是 ![]() .
.

(1)设 ![]() 到
到 ![]() 的距离为
的距离为 ![]() ,用
,用 ![]() 分别表示
分别表示 ![]() 到
到 ![]() 的距离,并求
的距离,并求 ![]() 的值;
的值;
(2)求目标 ![]() 的海防警戒线
的海防警戒线 ![]() 的距离(精确到
的距离(精确到 ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间[a,b]上的连续函数y=f(x),如果![]() ,使得
,使得![]() ,则称
,则称![]() 为区间[a,b]上的“中值点”,下列函数:
为区间[a,b]上的“中值点”,下列函数:
①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]() 中,在区间[O,1]上“中值点”多于一个的函数序号为( )
中,在区间[O,1]上“中值点”多于一个的函数序号为( )
A. ①② B. ①③ C. ②③ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线E:![]() ﹣
﹣![]() =1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
=1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
(1)求双曲线E的离心率;
(2)如图,O为坐标原点,动直线l分别交直线l1 , l2于A,B两点(A,B分别在第一、第四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有5名男生、2名女生站成一排照相,
(1)两女生要在两端,有多少种不同的站法?
(2)两名女生不相邻,有多少种不同的站法?
(3)女生甲不在左端,女生乙不在右端,有多少种不同的站法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() 的数据作了初步统计,得到如下数据:
的数据作了初步统计,得到如下数据:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年宣传费 | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() ,即
,即![]() .对上述数据作了初步处理,得到相关的值如下表:
.对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)规定当产品的年销售量![]() (吨)与年宣传费
(吨)与年宣传费![]() (万元)的比值在区间
(万元)的比值在区间![]() 内时认为该年效益良好.该公司某
内时认为该年效益良好.该公司某![]() 年投入的宣传费用(单位:万元)分别为:
年投入的宣传费用(单位:万元)分别为:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,试根据回归方程估计年销售量,从这
,试根据回归方程估计年销售量,从这![]() 年中任选
年中任选![]() 年,记其中选到效益良好年的数量为
年,记其中选到效益良好年的数量为![]() ,试求随机变量
,试求随机变量![]() 的分布列和期望.(其中
的分布列和期望.(其中![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com