
【题目】如图,三棱台![]() 的底面是正三角形,平面
的底面是正三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
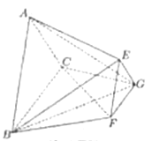
(Ⅰ)求证:![]() ;
;
(Ⅱ)若![]() 和梯形
和梯形![]() 的面积都等于
的面积都等于![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+2|x+1|.
(1)当a=2时,解不等式f(x)>4.
(2)若不等式f(x)<3x+4的解集是{x|x>2},求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为保护农民种粮收益,促进粮食生产,确保国家粮食安全,调动广大农民粮食生产的积极性,从2004年开始,国家实施了对种粮农民直接补贴.通过对2014~2018年的数据进行调查,发现某地区发放粮食补贴额![]() (亿元)与该地区粮食产量
(亿元)与该地区粮食产量![]() (万亿吨)之间存在着线性相关关系.统计数据如下表:
(万亿吨)之间存在着线性相关关系.统计数据如下表:
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
补贴额 | 9 | 10 | 12 | 11 | 8 |
粮食产量 | 23 | 25 | 30 | 26 | 21 |
(1)请根据如表所给的数据,求出![]() 关于
关于![]() 的线性回归直线方程
的线性回归直线方程![]() ;
;
(2)通过对该地区粮食产量的分析研究,计划2019年在该地区发放粮食补贴额7亿元,请根据(1)中所得的线性回归直线方程,预测2019年该地区的粮食产量.
(参考公式: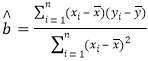 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业研制出一种型号为A的精密数控车床,A型车床为企业创造的价值逐年减少(以投产一年的年初到下一年的年初为A型车床所创造价值的第一年).若第 1 年A型车床创造的价值是250万元,且第1年至第6年,每年A型车床创造的价值减少30万元;从第7年开始,每年A型车床创造的价值是上一年价值的 50%.现用![]() (
(![]() )表示A型车床在第n年创造的价值.
)表示A型车床在第n年创造的价值.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)记![]() 为数列
为数列![]() 的前n项的和
的前n项的和![]()
![]() ,企业经过成本核算,若
,企业经过成本核算,若![]() 万元,则继续使用A型车床,否则更换A型车床,试问该企业须在第几年年初更换A型车床?(已知:若正数数列
万元,则继续使用A型车床,否则更换A型车床,试问该企业须在第几年年初更换A型车床?(已知:若正数数列![]() 是单调递减数列,则数列
是单调递减数列,则数列![]() 也是单调递减数列).
也是单调递减数列).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,证明直线
,证明直线![]() 与
与![]() 轴相交于定点
轴相交于定点![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.

(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,求这
个,求这![]() 个芒果中恰有
个芒果中恰有![]() 个在
个在![]() 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所以芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的长轴长为
的长轴长为![]() ,右顶点到左焦点的距离为
,右顶点到左焦点的距离为![]() ,直线l:
,直线l:![]() 与椭圆
与椭圆![]() 交于A,B两点.
交于A,B两点.

![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 若A为椭圆的上项点,M为AB中点,O为坐标原点,连接OM并延长交椭圆
若A为椭圆的上项点,M为AB中点,O为坐标原点,连接OM并延长交椭圆![]() 于N,
于N,![]() ,求k的值.
,求k的值.
![]() 若原点O到直线l的距离为1,
若原点O到直线l的距离为1,![]() ,当
,当![]() 时,求
时,求![]() 的面积S的范围.
的面积S的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com