
【题目】某投资公司在![]() 年年初准备将
年年初准备将![]() 万元投资到“低碳”项目上,现有两个项目供选择:
万元投资到“低碳”项目上,现有两个项目供选择:
项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利![]() ,也可能亏损
,也可能亏损![]() ,且这两种情况发生的概率分别为
,且这两种情况发生的概率分别为![]() 和
和![]() ;
;
项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利![]() ,可能损失
,可能损失![]() ,也可能不赔不赚,且这三种情况发生的概率分别为
,也可能不赔不赚,且这三种情况发生的概率分别为![]() 、
、![]() 和
和![]() .
.
针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由.
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的离心率为2,过点
的离心率为2,过点![]() 、斜率为1的直线
、斜率为1的直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点且
两点且![]() ,
,![]() .
.
(1)求双曲线方程。
(2)设![]() 为双曲线
为双曲线![]() 右支上动点,
右支上动点,![]() 为双曲线
为双曲线![]() 的右焦点,在
的右焦点,在![]() 轴负半轴上是否存在定点
轴负半轴上是否存在定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)在等腰直角三角形![]() 中,
中,![]() ,将
,将![]() 沿中位线
沿中位线![]() 翻折得到如图(2)所示的空间图形,使二面角
翻折得到如图(2)所示的空间图形,使二面角![]() 的大小为
的大小为![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只青蛙从数轴的原点出发,当投下的硬币正面向上时,它沿数轴的正方向跳动两个单位;当投下的硬币反面向上时,它沿数轴的负方向跳动一个单位,若青蛙跳动![]() 次停止,设停止时青蛙在数轴上对应的坐标为随机变量
次停止,设停止时青蛙在数轴上对应的坐标为随机变量![]() ,则
,则![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 轴为始边做两个锐角
轴为始边做两个锐角![]() ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]()
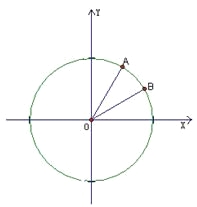
(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com