
【题目】某商场一年购进某种货物900吨,每次都购进x吨,运费为每次9万元,一年的总存储费用为9x万元.
(1)要使一年的总运费与总存储费用之和最小,则每次购买多少吨?
(2)要使一年的总运费与总存储费用之和不超过585万元,则每次购买量在什么范围?
【答案】
(1)解:设每次都购买x吨,则需要购买 ![]() 次,
次,
∵运费为9万/次,一年的总存储费用为9x万元,
∴一年的总运费与总存储费用之和为9× ![]() +9x万元
+9x万元
∵9× ![]() +9x≥540,当且仅当9×
+9x≥540,当且仅当9× ![]() =9x时取等号
=9x时取等号
∴x=30吨时,一年的总运费与总存储费用之和最小
(2)解:由题意,9× ![]() +9x≤585,得20≤x≤45.
+9x≤585,得20≤x≤45.
∴每次购买量在大于或等于20吨且小于或等于45吨的范围内
【解析】(1)先设某公司每次都购买x吨,由于一年购买某种货物900吨,得出需要购买的次数,从而求得一年的总运费与总存储费用之和,最后利用基本不等式求得一年的总运费与总存储费用之和最小即可.(2)根据一年的总运费与总存储费用之和不超过585万元,可建立不等式,从而可求次购买量的范围


科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体![]() 名学生中随机抽取了
名学生中随机抽取了![]() 名学生的体检表,并得到如图的频率分布直方图.
名学生的体检表,并得到如图的频率分布直方图.
年级名次 是否近视 |
|
|
近视 |
|
|
不近视 |
|
|
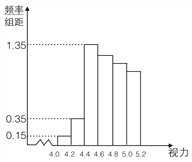
(1)若直方图中后四组的频数成等差数列,试估计全年级视力在![]() 以下的人数;
以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在![]() 名和
名和![]() 名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过
名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过![]() 的前提下认为视力与学习成绩有关系?
的前提下认为视力与学习成绩有关系?
(3)在(Ⅱ)中调查的![]() 名学生中,按照分层抽样在不近视的学生中抽取了
名学生中,按照分层抽样在不近视的学生中抽取了![]() 人,进一步调查他们良好的护眼习惯,并且在这
人,进一步调查他们良好的护眼习惯,并且在这![]() 人中任取
人中任取![]() 人,记名次在
人,记名次在![]() 的学生人数为
的学生人数为![]() ,求
,求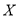 的分布列和数学期望.
的分布列和数学期望.
|
|
|
|
|
|
|
|
|
|
| 7.879 |
![]()
附: 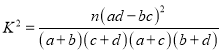
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时期赵爽在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示,我们教材中利用该图作为“( )”的几何解释. 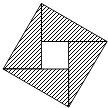
A.如果a>b,b>c,那么a>c
B.如果a>b>0,那么a2>b2
C.对任意实数a和b,有a2+b2≥2ab,当且仅当a=b时等号成立
D.如果a>b,c>0那么ac>bc
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(x,y)是区域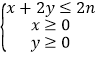 , (n∈N*)内的点,目标函数z=x+y,z的最大值记作zn . 若数列{an}的前n项和为Sn , a1=1,且点(Sn , an)在直线zn=x+y上.
, (n∈N*)内的点,目标函数z=x+y,z的最大值记作zn . 若数列{an}的前n项和为Sn , a1=1,且点(Sn , an)在直线zn=x+y上.
证明:数列{an﹣2}为等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学习兴趣小组开展“学生语文成绩与外语成绩的关系”的课题研究,考察该校高二年级800名学生上学期期末的语文和外语成绩,按是否优秀分类得结果:语文和外语成绩都优秀的有60人,语文成绩优秀但外语成绩不优秀的有140人,外语成绩优秀但语文成绩不优秀的有100人.
(Ⅰ)能否有![]() 的把握认为“该校学生语文成绩优秀与外语成绩是否优秀有关系”?
的把握认为“该校学生语文成绩优秀与外语成绩是否优秀有关系”?
(Ⅱ)将上述调查所得到的频率视为概率,从该校高二年级学生成绩中,有放回地随机抽取3名学生的成绩,记所抽取的成绩中,语文、外语两科成绩至少有一科优秀的人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
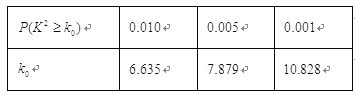
附:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2﹣4ax+3a2<0,其中a>0,命题q:实数x 满足![]() ;
;
(1)若a=1且p∧q为真,求实数x的取值范围;
(2)若q是p的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com