练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，曲线的方程为，以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为，点，点是曲线上的动点，为线段的中点.

    （1）写出曲线的参数方程，并求出点的轨迹的直角坐标方程；

    （2）已知点，直线与曲线的交点为，若线段的中点为，求线段长度.

    【答案】（1）（为参数）；；（2）.

    【解析】

    （1）根据圆的直角坐标方程写出曲线的参数方程，求出点的坐标，利用消参法求出点的轨迹的直角坐标方程；

    （2）将的参数方程为参数）代入曲线的直角坐标方程得，再利用直线参数方程的几何意义求解.

    （1）的参数方程为为参数）.

    设，所以，即的参数方程为为参数），化简为直角坐标方程为.

    所以点的轨迹的直角坐标方程为.

    （2）直线的直角坐标方程为，易知直线过点，

    设的参数方程为参数），将其代入曲线的直角坐标方程得，

    设对应的参数分别为，

    所以，

    所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】2020年寒假是特殊的寒假，因为疫情全体学生只能在家进行网上在线学习，为了研究学生在网上学习的情况，某学校在网上随机抽取120名学生对线上教育进行调查，其中男生与女生的人数之比为11∶13，其中男生30人对于线上教育满意，女生中有15名表示对线上教育不满意.

    （1）完成列联表，并回答能否有99%的把握认为对“线上教育是否满意与性别有关”；

    满意

    不满意

    总计

    男生

    女生

    合计

    120

    （2）从被调查中对线上教育满意的学生中，利用分层抽样抽取8名学生，再在8名学生中抽取3名学生，作线上学习的经验介绍，其中抽取男生的个数为，求出的分布列及期望值.

    参考公式：附：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    0.706

    3.841

    5.024

    6.635

    7.879

    10828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】棱台的三视图与直观图如图所示.

    （1）求证：平面平面；

    （2）在线段上是否存在一点，使与平面所成的角的正弦值为？若存在，指出点的位置；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，且曲线在处的切线平行于直线．

    （1）求a的值；

    （2）求函数的单调区间；

    （3）已知函数图象上不同的两点，试比较与的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设 （，）．

    （1）若展开式中第5项与第7项的系数之比为3∶8，求k的值；

    （2）设（），且各项系数，，，…，互不相同．现把这个不同系数随机排成一个三角形数阵：第1列1个数，第2列2个数，…，第n列n个数．设是第i列中的最小数，其中，且i，．记的概率为．求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）求的单调区间；

    （2）设曲线与轴正半轴的交点为，曲线在点处的切线方程为，求证：对于任意的实数，都有；

    （3）若方程为实数）有两个实数根，，且，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】A、B两人进行一局围棋比赛，A获得的概率为0.8，若采用三局两胜制举行一次比赛，现采用随机模拟的方法估计B获胜的概率.先利用计算器或计算机生成0到9之间取整数值的随机数，用0,1,2,3,4,5,6,7表示A获胜；8,9表示B获胜，这样能体现A获胜的概率为0.8.因为采用三局两胜制，所以每3个随机数作为一组.

    例如，产生30组随机数：034 743 738 636 964 736 614 698 637 162 332 616 804 560 111 410 959 774 246 762 428 114 572 042 533 237 322 707 360 751，据此估计B获胜的概率为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某种新型病毒的传染能力很强，给人们生产和生活带来很大的影响，所以创新研发疫苗成了当务之急.为此，某药企加大了研发投入，市场上这种新型冠状病毒的疫苗的研发费用（百万元）和销量（万盒）的统计数据如下：

    研发费用（百万元）

    2

    3

    6

    10

    13

    14

    销量（万盒）

    1

    1

    2

    2.5

    4

    4.5

    （1）根据上表中的数据，建立关于的线性回归方程（用分数表示）；

    （2）根据所求的回归方程，估计当研发费用为1600万元时，销售量为多少？

    参考公式：，.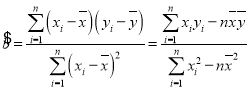

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，圆的方程为，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为．

    （1）求圆的极坐标方程与直线的直角坐标方程；

    （2）设直线与圆相交于，两点，求圆在，处两条切线的交点坐标．

    查看答案和解析>>

    同步练习册答案