
【题目】给出下列命题中
① 非零向量![]() 满足
满足![]() ,则
,则![]() 的夹角为
的夹角为![]() ;
;
② ![]()
![]() >0是
>0是![]() 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;
③若![]() 则
则![]() 必定是直角三角形;
必定是直角三角形;
④△ABC的外接圆的圆心为O,半径为1,若![]() ,且
,且![]() ,则向量
,则向量![]() 在向量
在向量![]() 方向上的投影为
方向上的投影为![]() .
.
以上命题正确的是 __________ (注:把你认为正确的命题的序号都填上)
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
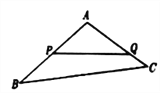
【题目】如图,某生态园将一块三角形地![]() 的一角
的一角![]() 开辟为水果园,已知角
开辟为水果园,已知角![]() 为
为![]() ,
, ![]() 的长度均大于200米,现在边界
的长度均大于200米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
(1)若围墙![]() 、
、![]() 总长度为200米,如何可使得三角形地块
总长度为200米,如何可使得三角形地块![]() 面积最大?
面积最大?
(2)已知竹篱笆长为![]() 米,
米, ![]() 段围墙高1米,
段围墙高1米, ![]() 段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(n)=n2cos(nπ),且an=f(n)+f(n+1),则a1+a2+a3+…+a100=( )
A.0
B.﹣100
C.100
D.10200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
(Ⅰ)在4月份任取一天,估计西安市在该天不下雨的概率;
(Ⅱ)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=7,a5+a7=26,数列{an}的前n项和为Sn .
(Ⅰ)求an;
(Ⅱ)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com