
【题目】在下图所示的几何体中,底面![]() 为正方形,
为正方形,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
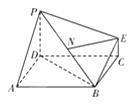
(1)证明:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)2.
【解析】试题分析: (1)证明线面垂直,一般利用线面垂直判定定理,即从线线垂直出发给予证明,其中线线垂直的寻找与论证从两个方面研究,一是利用立体中线面垂直关系转化,二是利用平几知识计算,本题先取![]() 中点
中点![]() ,转化证明
,转化证明![]() 平面
平面![]() ,由
,由![]() 平面
平面![]() 可得
可得![]() ,再由正方形性质可得
,再由正方形性质可得![]() .(2)求四棱锥体积,关键找高,而高的寻找往往利用线面垂直关系得到:
.(2)求四棱锥体积,关键找高,而高的寻找往往利用线面垂直关系得到:![]() 平面
平面![]() ,因此
,因此![]() 是四棱锥
是四棱锥![]() 的高,再代入体积公式即可.
的高,再代入体积公式即可.
试题解析:(1)连接![]() ,令
,令![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,因为点
,因为点![]() 是中点,
是中点,
∴![]() 且
且![]() .
.
又∵![]() 且
且![]() ,
,
∴![]() 且
且![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
∵四边形![]() 为正方形,∴
为正方形,∴![]() .
.
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
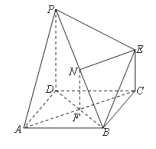
(2)∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
又∵![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() 是四棱锥
是四棱锥![]() 的高,
的高,
∵![]() ,
,
∴![]() ,
,
∴四棱锥![]() 的体积
的体积![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() 且
且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .证明:
.证明:![]() <0.
<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应阳光体育运动的号召,某县中学生足球活动正如火如荼地展开,该县为了解本县中学生的足球运动状况,根据性别采取分层抽样的方法从全县24000名中学生(其中男生14000人,女生10000人)中抽取120名,统计他们平均每天足球运动的时间,如下表:(平均每天足球运动的时间单位为小时,该县中学生平均每天足球运动的时间范围是![]() ).
).
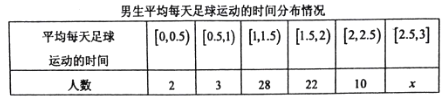
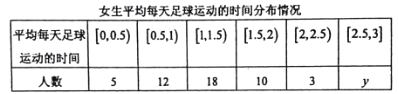
(1)请根据样本估算该校男生平均每天足球运动的时间(结果精确到0.1);
(2)若称平均每天足球运动的时间不少于2小时的学生为“足球健将”,低于2小时的学生为“非足球健将”.
①请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断,能否有90%的把握认为是否为“足球健将”与性别有关?
列联表,并通过计算判断,能否有90%的把握认为是否为“足球健将”与性别有关?
②若在足球运动时间不足1小时的男生中抽取2名代表了解情况,求这2名代表都是足球运动时间不足半小时的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.05 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 3.841 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)当![]() 时,若对任意互不相等的实数
时,若对任意互不相等的实数![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)判断函数![]() 在
在![]() 上的零点的个数,并说明理由.
上的零点的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行的“国际马拉松赛”,举办单位在活动推介晚会上进行嘉宾现场抽奖活动,抽奖盒中装有6个大小相同的小球,分别印有“快乐马拉松”和“美丽绿城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球(取出后不再放回),若抽到的两个球都印有“快乐马拉松”标志即可获奖.并停止取球;否则继续抽取,第一次取球就抽中获一等奖,第二次取球抽中获二等奖,第三次取球抽中获三等奖,没有抽中不获奖.活动开始后,一位参赛者问:“盒中有几个印有‘快乐马拉松’的小球?”主持人说:“我只知道第一次从盒中同时抽两球,不都是‘美丽绿城行’标志的概率是
(1)求盒中印有“快乐马拉松”小球的个数;
(2)若用![]() 表示这位参加者抽取的次数,求
表示这位参加者抽取的次数,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(λx+1)ln x-x+1.
(1)若λ=0,求f(x)的最大值;
(2)若曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直,证明:![]() >0.
>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,将木兰溪流经市区河段分成![]() 段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如下表:
段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如下表:
南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
(Ⅰ)记评分在![]() 以上(包括
以上(包括![]() )为优良,从中任取一段,求在同一段中两岸环保评分均为优良的概率;
)为优良,从中任取一段,求在同一段中两岸环保评分均为优良的概率;
(Ⅱ)根据表中数据完成下面茎叶图;
(Ⅲ)分别估计两岸分值的中位数,并计算它们的平均值,试从计算结果分析两岸环保情况,哪边保护更好.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com