
【题目】设函数![]() ,
,![]() a为实数
a为实数![]() ,
,
![]() 求函数
求函数![]() 的单调区间;
的单调区间;
![]() 若存在实数a,使得
若存在实数a,使得![]() 对任意
对任意![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.![]() 提示:
提示:![]()
【答案】(1)![]() 单调递减,
单调递减,![]() 单调递增;(2)
单调递增;(2)![]()
【解析】
(1)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)令
的减区间;(2)令![]() ,
,![]() 时,不合题意,
时,不合题意,![]() 时,利用导数求得
时,利用导数求得![]() ,问题等价于
,问题等价于![]() 恒成立,再利用导数求得
恒成立,再利用导数求得![]() 的最大值即可得结果.
的最大值即可得结果.
(1)![]() ,
,
由![]() ,得
,得![]() ,
,
![]() ,得
,得![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)令![]() ,
,
则![]() ,
,
若e-a≥0,可得h′(x)>0,函数h(x)为增函数,当x→+∞时,h(x)→+∞,
不满足h(x)≤0对任意x∈R恒成立;
若e-a<0,由h’(x)=0,得![]() ,则
,则![]() ,
,
∴当x∈![]() 时,h′(x)>0,当x∈
时,h′(x)>0,当x∈![]() 时,h′(x)<0,
时,h′(x)<0,
∴![]() ,
,
若f(x)≤g(x)对任意x∈R恒成立, 则![]() ≤0(a>e)恒成立,
≤0(a>e)恒成立,
若存在实数a,使得![]() ≤0成立, 则ma≥
≤0成立, 则ma≥![]() ,
,
∴![]() (a>e),
(a>e),
令F(a)![]() , 则
, 则![]() .
.
∴当a<2e时,F′(a)<0,当a>2e时,F′(a)>0,
则![]() .
.
∴m![]() . 则实数m的取值范围是
. 则实数m的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】有下列几个命题:①若![]() ,则
,则![]() ;②“若
;②“若![]() ,则
,则![]() 互为相反数”的否命题“;③“若
互为相反数”的否命题“;③“若![]() 则
则![]() ”的逆命题;④“若
”的逆命题;④“若![]() ,则
,则![]() 互为倒数”的逆否命题. 其中真命题的序号__________.
互为倒数”的逆否命题. 其中真命题的序号__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地统计局调查了10000名居民的月收入,并根据所得数据绘制了样本的频率分布直方图如图所示。
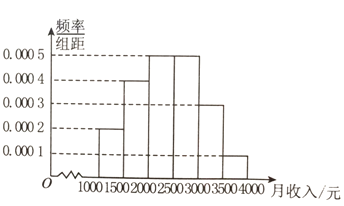
(1)求居民月收入在[3000,3500)内的频率;
(2)根据频率分布直方图求出样本数据的中位数;
(3)为了分析居民的月收入与年龄、职业等方面的关系,必须按月收入再从这10000中用分层抽样的方法抽出100人做进一步分析,则应从月收入在[2500,3000)内的居民中抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1=![]() ,(n∈N*)
,(n∈N*)
(1)求数列{an}的通项公式an,
(2)若数列{bn}满足bn=(3n﹣1)![]() an,数列{bn}的前n项和为Tn,若不等式(﹣1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
an,数列{bn}的前n项和为Tn,若不等式(﹣1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在正三棱柱![]() 中,侧棱长
中,侧棱长![]() 为3,H、G分别是AB,
为3,H、G分别是AB,![]() 中点.
中点.
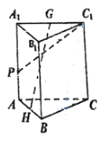
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求此三棱柱的侧面积;
,求此三棱柱的侧面积;
(3)若P为侧棱![]() 上一点,且
上一点,且![]() ,
,![]() 与平面
与平面![]() 所成角大小为
所成角大小为![]() ,求此三棱柱的体积.
,求此三棱柱的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣4x+3=0,过原点的直线l与圆C有公共点.
(1)求直线l斜率k的取值范围;
(2)已知O为坐标原点,点P为圆C上的任意一点,求线段OP的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年我国全面建成小康社会,其中小康生活的住房标准是城镇人均住房建筑面积30平方米. 下表为2007年—2016年中,我区城镇和农村人均住房建筑面积统计数据. 单位:平方米.
2007年 | 2008年 | 2009年 | 2010年 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
城镇 | 18.66 | 20.25 | 22.79 | 25 | 27.1 | 28.3 | 31.6 | 32.9 | 34.6 | 36.6 |
农村 | 23.3 | 24.8 | 26.5 | 27.9 | 30.7 | 32.4 | 34.1 | 37.1 | 41.4 | 45.8 |
(1)现从上述表格中随机抽取一年数据,试估计该年城镇人均住房建筑面积达到小康生活住房标准的概率;
(2)现从上述表格中随机抽取连续两年数据,求这两年中城镇人均住房建筑面积增长不少于2平方米的概率;
(3)将城镇和农村的人均住房建筑面积经四舍五入取整后作为样本数据.记2012—2016年中城镇人均住房面积的方差为![]() ,农村人均住房面积的方差为
,农村人均住房面积的方差为![]() ,判断
,判断![]() 与
与![]() 的大小.(只需写出结论).
的大小.(只需写出结论).
(注:方差![]() ,其中
,其中![]() 为
为 ![]()
![]() ,……
,…… ![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是椭圆
是椭圆![]() 的一个顶点,
的一个顶点,![]() 的短轴是圆
的短轴是圆![]() 的直径,直线
的直径,直线![]() ,
,![]() 过点P且互相垂直,
过点P且互相垂直,![]() 交椭圆
交椭圆![]() 于另一点D,
于另一点D,![]() 交圆
交圆![]() 于A,B两点
于A,B两点
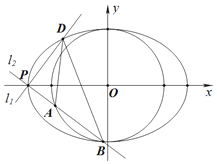
![]() Ⅰ
Ⅰ![]() 求椭圆
求椭圆![]() 的标准方程;
的标准方程;
![]() Ⅱ
Ⅱ![]() 求
求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com