

| A. | 当CD为Rt△ABC的中线时,d取得最小值 | |
| B. | 当CD为Rt△ABC的角平分线时,d取得最小值 | |
| C. | 当CD为Rt△ABC的高线时,d取得最小值 | |
| D. | 当D在Rt△ABC的AB边上移动时,d为定值 |
分析 过A作CD的垂线AG,过B作CD的延长线的垂线BH,设BC=a,AC=b,∠ACD=θ,利用两条异面直线上两点间的距离转化为含有θ的三角函数求得最值.
解答 解:如图,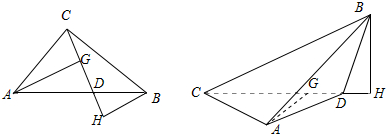
设BC=a,AC=b,∠ACD=θ,则$∠BCD=\frac{π}{2}-θ$(0$<θ<\frac{π}{2}$),
过A作CD的垂线AG,过B作CD的延长线的垂线BH,
∴AG=bsinθ,BH=acosθ,CG=bcosθ,CH=asinθ,则HG=CH-CG=asinθ-bcosθ,
∴d=|AB|=$\sqrt{A{G}^{2}+B{H}^{2}+H{G}^{2}}$=$\sqrt{{b}^{2}si{n}^{2}θ+{a}^{2}co{s}^{2}θ+(asinθ-bcosθ)^{2}}$
=$\sqrt{{b}^{2}si{n}^{2}θ+{a}^{2}co{s}^{2}θ+{a}^{2}si{n}^{2}θ+{b}^{2}co{s}^{2}θ-absin2θ}$=$\sqrt{{a}^{2}+{b}^{2}-absin2θ}$.
∴当$θ=\frac{π}{4}$,即当CD为Rt△ABC的角平分线时,d取得最小值.
故选:B.
点评 本题考查平面与平面之间的位置关系,考查了两条异面直线上两点间的距离,运用数学转化思想方法是解答该题的关键,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-12,6] | B. | [-6,12] | C. | [-3,12] | D. | [6,12] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 所取球的情况 | 三个球均为红色 | 三个球均不同色 | 恰有两球为红色 | 其他情况 |
| 所获得的积分 | 180 | 90 | 60 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com