
分析 (1)由e=$\frac{c}{a}$=$\frac{1}{3}$,即a=3c,9-(-c)=10,则c=1,a=3,b2=a2-c2=8,即可求得椭圆的方程;
(2)由向量数量积的坐标运算$\overrightarrow{PE}•\overrightarrow{PF}={\overrightarrow{PN}^2}-1={(x-1)^2}+{y^2}-1={(x-1)^2}+(8-\frac{8}{9}{x^2})-1={(\frac{1}{3}x-3)^2}-1$,由(1)可知,即可求得$\overrightarrow{PE}•\overrightarrow{PF}$的取值范围;
(3)设圆M(x-m)2+(y-n)2=r2(r>0),其中$\frac{m^2}{9}+\frac{n^2}{8}=1$,由于$\frac{|NF|}{|NT|}=\sqrt{2}$,则x2+y2-6x-1=0,代入得2(m-3)x+2ny-m2-n2+r2-1=0对圆M上任意点N恒成立,即可求得m和n,求得圆M的方程.
解答 解:(1)由椭圆的焦点在x轴上,e=$\frac{c}{a}$=$\frac{1}{3}$,即a=3c,
由左焦点F(-c,0)到直线l:x=9的距离为10,即9-(-c)=10,则c=1,
a=3,b2=a2-c2=8,
椭圆的方程$\frac{x^2}{9}+\frac{y^2}{8}=1$;…(3分)
(2)由$\overrightarrow{PE}•\overrightarrow{PF}={\overrightarrow{PN}^2}-1={(x-1)^2}+{y^2}-1={(x-1)^2}+(8-\frac{8}{9}{x^2})-1={(\frac{1}{3}x-3)^2}-1$,
∵-3≤x≤3,
∴$\overrightarrow{PE}•\overrightarrow{PF}∈[3,15]$,
即$\overrightarrow{PE}•\overrightarrow{PF}$的取值范围是[3,15];…(8分)
(3)设圆M(x-m)2+(y-n)2=r2(r>0),其中$\frac{m^2}{9}+\frac{n^2}{8}=1$,
则x2+y2=2mx+2ny-m2-n2+r2. …(10分)
由于$\frac{|NF|}{|NT|}=\sqrt{2}$,则(x+1)2+y2=2[(x-1)2+y2-1],…(12分)
即x2+y2-6x-1=0,代入x2+y2=2mx+2ny-m2-n2+r2,
得2(m-3)x+2ny-m2-n2+r2-1=0对圆M上任意点N恒成立.
只要使$\left\{\begin{array}{l}m-3=0\\ n=0\\{r^2}={m^2}+{n^2}+1\end{array}\right.$,即$\left\{\begin{array}{l}m=3\\ n=0\\ r=\sqrt{10}\end{array}\right.$,
经检验满足$\frac{m^2}{9}+\frac{n^2}{8}=1$,故存在符合条件的圆,它的方程是(x-3)2+y2=10. …(15分)
点评 本题考查椭圆的标准方程及简单几何性质,向量数量积的坐标运算,圆的性质,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{4}$ | B. | $\frac{5\sqrt{5}}{4}$ | C. | $\frac{41}{20}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+(y+1)2=18 | B. | (x+1)2+y2=9 | C. | (x+1)2+y2=18 | D. | x2+(y+1)2=9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
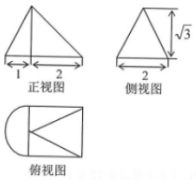
| A. | 8+$\frac{π}{2}$+$\sqrt{7}$ | B. | 8+$\frac{3π}{2}$+$\sqrt{7}$ | C. | 6+$\frac{3π}{2}$+$\sqrt{3}$ | D. | 6+$\frac{π}{2}$+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,G分别是PA,PB,BC的中点;
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,G分别是PA,PB,BC的中点;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com