分析:通过建立空间直角坐标系,(1)利用异面直线的方向向量所成的夹角即可得出;(2)求出平面BDC
1的法向量,利用点C到平面BDC
1的距离公式d=
即可得出;
(3)求出平面CDD
1C
1的法向量,利用sinθ=
|cos<,>|=
即可得出.
解答:解:(1)如图所示,

建立空间直角坐标系.
则A
1(0,0,0),B
1(1,0,0),C
1(1,1,0),D
1(0,1,0),A(0,0,2),B(1,0,2),C(1,1,2),D(0,1,2),
∴
=(-1,1,0),
=(1,0,-2).
∴
cos<,>=
=
=
-.
∴异面直线BD与AB
1所成角=
arccos.
(2)由(1)可知:
=(0,1,0),
=(-1,0,2).
设平面BDC
1的法向量为
=(x,y,z),
则
,即
,令z=1,则x=2,y=2.
∴
=(2,2,1).
∴点C到平面BDC
1的距离d=
=
=
.
(3)由(1)可知:
=(-1,1,2).
∵A
1D
1⊥平面CDD
1C
1,∴可取
=(0,1,0)作为平面CDD
1C
1的法向量.
设直线B
1D与平面CDD
1C
1所成的角为θ.
则sinθ=
|cos<,>|=
=
=
.
点评:熟练掌握通过建立空间直角坐标系、由异面直线的方向向量所成的夹角求异面直线所成的角、点C到平面BDC
1的距离公式d=
、由sinθ=
|cos<,>|=
求线面角是解题的关键.

 已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,高AA1=2,
已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,高AA1=2, 建立空间直角坐标系.
建立空间直角坐标系.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案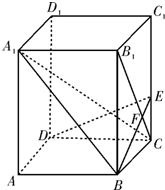 如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1,
如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1,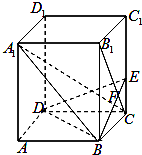 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.