
分析 由题意画出图形,求出A的坐标,结合向量等式求得C的坐标,代入椭圆方程可解e的值.
解答 解:如图,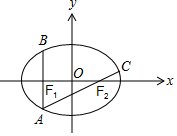
由题意,A(-c,$-\frac{{b}^{2}}{a}$),
∵$\overrightarrow{A{F}_{2}}$=2$\overrightarrow{{F}_{2}C}$,∴${y}_{C}=\frac{{b}^{2}}{2a}$,且xC-c=c,得xC=2c.
∴C(2c,$\frac{{b}^{2}}{2a}$),代入椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,
得$\frac{4{c}^{2}}{{a}^{2}}+\frac{{b}^{2}}{4{a}^{2}}=1$,即5c2=a2,解得e=$\frac{\sqrt{5}}{5}$.
故答案为:$\frac{{\sqrt{5}}}{5}$.
点评 本题考查椭圆的简单性质,考查了平面向量在求解圆锥曲线问题中的应用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
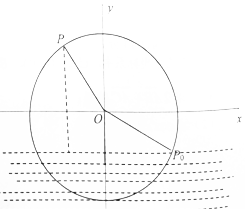 一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).
一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{25}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
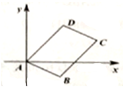 如图,面积为8的平行四边形ABCD,A为坐标原点,B坐标为(2,-1),C、D均在第一象限.
如图,面积为8的平行四边形ABCD,A为坐标原点,B坐标为(2,-1),C、D均在第一象限.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com