
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C的离心率为![]() ,且椭圆C过点
,且椭圆C过点![]() .
.
(1)求椭圆C的标准方程:
(2)若直线l:![]() 与椭圆C相交于A,B两点(A,B不是左右顶点),且以
与椭圆C相交于A,B两点(A,B不是左右顶点),且以![]() 为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
科目:高中数学 来源: 题型:
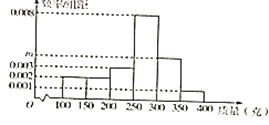
【题目】炎炎夏季,水蜜桃成为备受大家欢迎的一种水果,某果园的水蜜桃质量分布如图所示.
(Ⅰ)求m的值;
(Ⅱ)以频率估计概率,若从该果园中随机采摘5个水蜜桃,记质量在300克以上(含300克)的个数为X,求X的分布列及数学期望;
(Ⅲ)经市场调查,该种水蜜桃在过去50天的销售量(单位:千克)和价格(单位:元/千克)均为销售时间t(天)的函数,且销售量近似地满足f(t)=﹣3t+300(1≤t≤50,t∈N),前30天价格为g(t)=![]() +20(1≤t≤30,t∈N),后20天价格为g(t)=30(31≤t≤50,t∈N),求日销售额S的最大值.
+20(1≤t≤30,t∈N),后20天价格为g(t)=30(31≤t≤50,t∈N),求日销售额S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆的焦点且与长轴垂直的弦长为1.
,过椭圆的焦点且与长轴垂直的弦长为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上第一象限内一动点,A,B分别为椭圆的左顶点和下顶点,直线MB与x轴交于点C,直线MA与y轴交于点D,求证:四边形ABCD的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的“局部对称点”.
的“局部对称点”.
(1)![]() ,其中
,其中![]() ,试判断
,试判断![]() 是否有“局部对称点”?若有,请求出该点;若没有,请说明理由;
是否有“局部对称点”?若有,请求出该点;若没有,请说明理由;
(2)若函数![]() 在区间
在区间![]() 内有“局部对称点”,求实数m的取值范围;
内有“局部对称点”,求实数m的取值范围;
(3)若函数![]() 在R上有“局部对称点”,求实数m的取值范围.
在R上有“局部对称点”,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若给定非零实数
,若给定非零实数![]() ,对于任意实数
,对于任意实数![]() ,总存在非零常数
,总存在非零常数![]() ,使得
,使得![]() 恒成立,则称函数
恒成立,则称函数![]() 是
是![]() 上的
上的![]() 级
级![]() 类周期函数,若函数
类周期函数,若函数![]() 是
是![]() 上的2级2类周期函数,且当
上的2级2类周期函数,且当![]() 时,
时,![]() ,又函数
,又函数![]() .若
.若![]() ,
,![]() ,使
,使![]() 成立,则实数
成立,则实数![]() 的取值范围是_______.
的取值范围是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人,不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人,则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com