
【题目】如图所示,公园内有一块边长为![]() 的等边
的等边![]() 形状的三角地,现修成草坪,图中
形状的三角地,现修成草坪,图中![]() 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分,![]() 在
在![]() 上,
上,![]() 在
在![]() 上.
上.
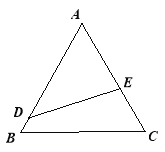
(Ⅰ)设![]()
![]() ,试用
,试用![]() 表示
表示![]() 的函数关系式;
的函数关系式;
(Ⅱ)如果![]() 是灌溉水管,为节约成本希望它最短,
是灌溉水管,为节约成本希望它最短,![]() 的位置应该在哪里?如果
的位置应该在哪里?如果![]() 是参观线路,则希望它最长,
是参观线路,则希望它最长,![]() 的位置又在哪里?请给予证明.
的位置又在哪里?请给予证明.
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】某班有50名学生,一次考试后数学成绩ξ~N(110,102),若P(100≤ξ≤110)=0.34,则估计该班学生数学成绩在120分以上的人数为 ( )
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}前三项的和为﹣3,前三项的积为8.
(I)求等差数列{an}的通项公式;
(II)若a2 , a3 , a1成等比数列,求数列{|an|}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构观察了某地100个新生婴儿的体重,并根据所得数据画出了样本的频率分布直方图如图,则新生婴儿的体重在[3.2,4.0)(kg)的有人.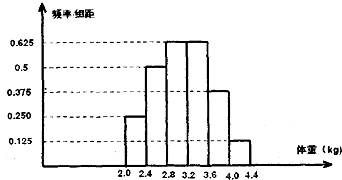
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)过点
=1(a>b>0)过点 ![]() ,且离心率e为
,且离心率e为 ![]() .
.
(1)求椭圆E的方程;
(2)设直线x=my﹣1(m∈R)交椭圆E于A,B两点,判断点G ![]() 与以线段AB为直径的圆的位置关系,并说明理由.
与以线段AB为直径的圆的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生社团对本校学生学习方法开展问卷调查的过程中发现,在回收上来的1000份有效问卷中,同学们背英语单词的时间安排有两种:白天背和晚上临睡前背。为研究背单词时间安排对记忆效果的影响,该社团以5%的比例对这1000名学生按时间安排进行分层抽样,并完成一项试验,试验方法是:使两组学生记忆40个无意义音节(如xiq,geh),均要求刚能全部记清就停止识记,并在8小时后进行记忆测验。不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验。两组同学识记停止8小时后的准确回忆(保持)情况如图(区间含左端点不含右端点)。
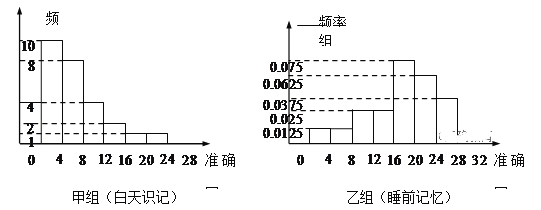
(1)估计1000名被调查的学生中识记停止8小时后40个音节的保持率大于或等于60%的人数;
(2)从乙组准确回忆个数在![]() 范围内的学生中随机选3人,记:能准确回忆20个以上(含20)的人数为随机变量X,求X的分布列及数学期望;
范围内的学生中随机选3人,记:能准确回忆20个以上(含20)的人数为随机变量X,求X的分布列及数学期望;
(3)从本次试验的结果来看,上述两种时间安排方法中哪种方法背英语单词记忆效果更好?计算并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形的四个顶点A(﹣1,﹣1),B(1,﹣1),C(1,1),D(﹣1,1)分别在抛物线y=﹣x2和y=x2上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在图中阴影区域的概率是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,E是棱DD1的中点.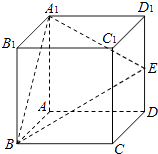
(1)求直线BE与平面ABB1A1所成的角的正弦值;
(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆G:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,经过左焦点F1(-1,0)的直线l与椭圆G相交于A,B两点,与y轴相交于点C,且点C在线段AB上.
,经过左焦点F1(-1,0)的直线l与椭圆G相交于A,B两点,与y轴相交于点C,且点C在线段AB上.
(1)求椭圆G的方程;
(2)若|AF1|=|CB|,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com