
 和
和 不共线.
不共线. =
= +
+ ,
, =
=
 ,
, =
=
 ,求证:A、B、D三点共线;
,求证:A、B、D三点共线; =2,
=2, =3,
=3, 与
与 的夹角为60°,是否存在实数m,使得m
的夹角为60°,是否存在实数m,使得m
 与
与
 垂直?
垂直?科目:高中数学 来源:广州省2009-2010学年高一学科竞赛 题型:解答题
设两个非零向量 和
和 不共线;
不共线;
(1)试确定实数 ,使
,使 和
和 共线;
共线;
(2)若 ,
, ,
, 与
与 的夹角为60°,试确定
的夹角为60°,试确定 ,使
,使 与
与 垂直。
垂直。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 和
和 不共线.
不共线. =
= +
+ ,
, =
=
 ,
, =
=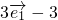
 ,求证:A、B、D三点共线;
,求证:A、B、D三点共线;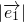 =2,
=2,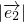 =3,
=3, 与
与 的夹角为60°,是否存在实数m,使得m
的夹角为60°,是否存在实数m,使得m
 与
与
 垂直?
垂直?查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省惠州一中高一(上)第二次月考数学试卷(解析版) 题型:解答题
 ;
; 和
和 不共线,且
不共线,且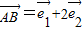 ,
,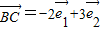 ,
, ,求证:A,B,D三点在同一直线上.
,求证:A,B,D三点在同一直线上.查看答案和解析>>
科目:高中数学 来源:2010-2011学年安徽省亳州二中高一(下)数学试卷(必修4)(解析版) 题型:解答题
 ,求
,求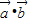 的值;
的值; 和
和 不共线.如果
不共线.如果 =
=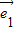 +
+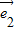 ,
, =
=
 ,
, =
=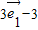
 ,
,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com