
| 3 |
| 2 |
| 3 |
| 2 |
|
| 1 |
| 4 |
| 1 |
| m |
| 1 |
| m |
| 1 |
| m |
| x |
| x2+1 |
| x |
| x2+1 |
| 1 | ||
x+
|
| 1 |
| x |
| 1 | ||
x+
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:
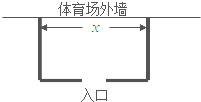 备受瞩目的巴西世界杯正在如火如荼的进行,为确保总决赛的顺利进行,组委会决定在位于里约热内卢的马拉卡纳体育场外临时围建一个矩形观众候场区,总面积为72m2(如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为2m的入口.现已知铁栏杆的租用费用为100元/m.设该矩形区域的长为x(单位:m),租用铁栏杆的总费用为y(单位:元)
备受瞩目的巴西世界杯正在如火如荼的进行,为确保总决赛的顺利进行,组委会决定在位于里约热内卢的马拉卡纳体育场外临时围建一个矩形观众候场区,总面积为72m2(如图所示).要求矩形场地的一面利用体育场的外墙,其余三面用铁栏杆围,并且要在体育馆外墙对面留一个长度为2m的入口.现已知铁栏杆的租用费用为100元/m.设该矩形区域的长为x(单位:m),租用铁栏杆的总费用为y(单位:元)查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com