
【题目】已知定义在R上的函数 ![]() ,若函数g(x)=f(x)﹣a(x+1)恰有2个零点,则实数a的取值范围是 .
,若函数g(x)=f(x)﹣a(x+1)恰有2个零点,则实数a的取值范围是 .
【答案】![]() ∪{0}
∪{0}
【解析】解:数形结合,由直线y=a(x+1)与曲线y=f(x)的位置关系如图:x≤﹣1时,y=x2+x,y′=2x+1, ![]() =﹣1,
=﹣1,
函数g(x)=f(x)﹣a(x+1)恰有2个零点,可得a≤﹣1;
当x∈(﹣1,0)时,y=﹣x2﹣x,y′=﹣2x﹣1, ![]() =2﹣1=1;
=2﹣1=1;
当x>0时,y=ln(x+1),过(﹣1,0)点与曲线的切点为:(m,ln(m+1)),
y′= ![]() ,
,
可得: ![]() =
= ![]() ,可得m=e﹣1,
,可得m=e﹣1,
切线的斜率为: ![]() .函数g(x)=f(x)﹣a(x+1)恰有2个零点,可得a
.函数g(x)=f(x)﹣a(x+1)恰有2个零点,可得a ![]() ,
,
a=0时,函数的零点也是2个.
综上可得当 ![]() ∪{0}时有两个交点,即函数y=g(x)恰有两个零点.
∪{0}时有两个交点,即函数y=g(x)恰有两个零点.
所以答案是: ![]() ∪{0}.
∪{0}.
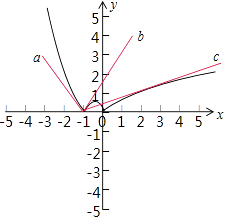


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,x∈R,ω>0.
,x∈R,ω>0.
(1)求函数f(x)的值域;
(2)若函数y=f(x)的图象与直线y=﹣1的两个相邻交点间的距离为 ![]() ,求函数y=f(x)的单调区间.
,求函数y=f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上存在导数f′(x),x∈R,有f(﹣x)+f(x)=x2 , 在(0,+∞)上f′(x)<x,若f(4﹣m)﹣f(m)≥8﹣4m.则实数m的取值范围为( )
A.[﹣2,2]
B.[2,+∞)
C.[0,+∞)
D.(﹣∞,﹣2]∪[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于实数a,b,c,下列命题正确的是( )
A.若a>b,则ac2>bc2
B.若a<b<0,则a2>ab>b2
C.若a<b<0,则 ![]()
D.若a<b<0,则 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工艺品厂要设计一个如图1所示的工艺品,现有某种型号的长方形材料如图2所示,其周长为4m,这种材料沿其对角线折叠后就出现图1的情况.如图,ABCD(AB>AD)为长方形的材料,沿AC折叠后AB'交DC于点P,设△ADP的面积为S2 , 折叠后重合部分△ACP的面积为S1 .
(Ⅰ)设AB=xm,用x表示图中DP的长度,并写出x的取值范围;
(Ⅱ)求面积S2最大时,应怎样设计材料的长和宽?
(Ⅲ)求面积(S1+2S2)最大时,应怎样设计材料的长和宽?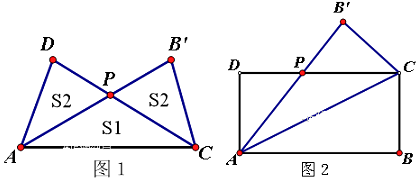
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2﹣ax+a)e﹣x , a∈R.
(1)求函数f(x)的单调区间;
(2)设g(x)=f'(x),其中f'(x)为函数f(x)的导函数.判断g(x)在定义域内是否为单调函数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (a>0). (Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(a>0). (Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若 ![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(Ⅲ)证明:总存在x0 , 使得当x∈(x0 , +∞),恒有f(x)<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 ![]() (t为参数).
(t为参数).
(Ⅰ)写出直线l的普通方程与曲线C的直角坐标方程;
(Ⅱ)设曲线C经过伸缩变换 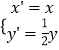 得到曲线C',若点P(1,0),直线l与C'交与A,B,求|PA||PB|,|PA|+|PB|.
得到曲线C',若点P(1,0),直线l与C'交与A,B,求|PA||PB|,|PA|+|PB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com