
 万元,年维修费用第一年是
万元,年维修费用第一年是 万元,第二年是
万元,第二年是 万元,第三年是
万元,第三年是 万元,…,以后逐年递增
万元,…,以后逐年递增 万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用
万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用 年的维修费用的和为
年的维修费用的和为 ,年平均费用为
,年平均费用为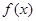 .
. ,
,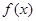 的解析式;
的解析式; ,
, ;(2)
;(2) 时,年平均费用最小,最小值为3万元.
时,年平均费用最小,最小值为3万元.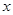 年的维修费用的和为
年的维修费用的和为 ,而第一年的维修费用是
,而第一年的维修费用是 万元,以后逐年递增
万元,以后逐年递增 万元,每一年的维修费用形成以
万元,每一年的维修费用形成以 为首项,
为首项, 为公差的等差数列,根据等差数列的前
为公差的等差数列,根据等差数列的前 项和即可求出
项和即可求出 的解析式;将购车费、每年使用的保险费、养路费、汽油费以及维修费用之和除以
的解析式;将购车费、每年使用的保险费、养路费、汽油费以及维修费用之和除以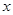 即可得到年平均费用
即可得到年平均费用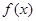 ,根据基本不等式即可求出平均费用的最小值.
,根据基本不等式即可求出平均费用的最小值.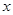 年的维修费用的和为
年的维修费用的和为 ,而第一年的维修费用是
,而第一年的维修费用是 万元,以后逐年递增
万元,以后逐年递增 万元,每一年的维修费用形成以
万元,每一年的维修费用形成以 为首项,
为首项, 为公差的等差数列,根据等差数列的前
为公差的等差数列,根据等差数列的前 项和公式可得:
项和公式可得:
 ,
, ;
;
 即
即 时,年平均费用最小,最小值为3万元.
时,年平均费用最小,最小值为3万元. 项和公式以的掌握,以及基本不等式的应用,同时考查了学生解决实际应用题的能力.
项和公式以的掌握,以及基本不等式的应用,同时考查了学生解决实际应用题的能力.

科目:高中数学 来源:不详 题型:解答题
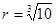 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.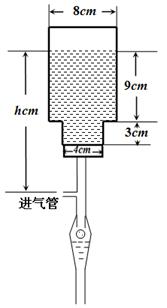
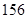 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?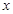 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为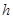 (单位:厘米),已知当
(单位:厘米),已知当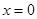 时,
时,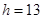 .试将
.试将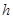 表示为
表示为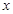 的函数.(注:
的函数.(注: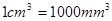 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
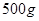 ,按每年
,按每年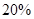 衰减.
衰减.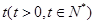 年后,这种放射性元素的质量
年后,这种放射性元素的质量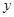 与
与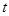 的函数关系式;
的函数关系式; 时所经历的时间).(
时所经历的时间).(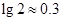 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 m,盖子边长为
m,盖子边长为 m,
m,
 关于
关于 的解析式;
的解析式;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的函数
的函数 ,如果同时满足以下三个条件:
,如果同时满足以下三个条件:  ,总有
,总有 ;②
;② ;③若
;③若 都有
都有 成立;
成立;  为
为 函数.
函数. 为
为 函数,则
函数,则 ;(2)函数
;(2)函数 是
是 函数;
函数; 为
为 函数,假定存在
函数,假定存在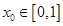 ,使得
,使得 ,且
,且 , 则
, 则 ; 其中真命题是________.(填上所有真命题的序号)
; 其中真命题是________.(填上所有真命题的序号)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的图象上, 那么称[A, B]为函数f(x)的一组关于原点的中心对称点 ([A , B]与[B, A]看作一组). 函数
的图象上, 那么称[A, B]为函数f(x)的一组关于原点的中心对称点 ([A , B]与[B, A]看作一组). 函数 关于原点的中心对称点的组数为_____________
关于原点的中心对称点的组数为_____________查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
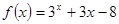 ,用二分法求方程
,用二分法求方程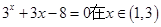 内近似解的过程中,取区间中点
内近似解的过程中,取区间中点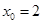 ,那么下一个有根区间为 ( )
,那么下一个有根区间为 ( )| A.(1,2) | B.(2,3) |
| C.(1,2)或(2,3)都可以 | D.不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com