
已知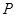 是双曲线
是双曲线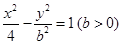 上一点,
上一点,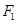 、
、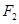 是其左、右焦点,
是其左、右焦点,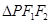 的三边长成等差数列,且
的三边长成等差数列,且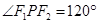 ,则双曲线的离心率等于
,则双曲线的离心率等于
A. | B.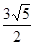 | C.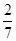 | D. |
D
解析试题分析:由题意,可根据双曲线的定义及题设中三边长度成等差数列得出方程|PF1|-|PF2|=4与2|PF1|=|PF2|+2c,由此两方程可解出|PF1|=2c-4,|PF2|=2c-8,再由∠F1 P F2=120°,由余弦定理建立关于c的方程,解出c的值,即可由公式求出离心率的值. 解:由题,不妨令点P在右支上,如图,则有,|PF1|-|PF2|=4 ①,2|PF1|=|PF2|+2c ②,由①②解得|PF1|=2c-4,|PF2|=2c-8,又∠F1 P F2=120°,由余弦定理得,4c2=(2c-4)2+(2c-8)2+(2c-4)×(2c-8),解得,c=7或c=2(舍),又a=2,故e= 故答案为 D
故答案为 D
考点:双曲线的简单性质
点评:本题考查双曲线的简单性质及等差数列的性质,解题的关键是熟练掌握基础知识且能灵活选用基础知识建立方程求参数,本题考查了方程的思想及转化的思想


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:单选题
P是双曲线 的右支上一点,M、N分别是圆(x+5)2+y2=4和
的右支上一点,M、N分别是圆(x+5)2+y2=4和
(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( ).
| A.6 | B.7 | C.8 | D.9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com