
分析 (1)利用向量数量积的公式化简函数f(x)即可.
(2)求出函数f(x)的表达式,利用换元法结合一元二次函数的最值性质进行讨论求解即可.
(3)由g(x)=0得到方程的根,利用三角函数的性质进行求解即可.
解答 解:(1)$\overrightarrow{a}$•$\overrightarrow{b}$=(cos$\frac{3x}{2}$,sin$\frac{3x}{2}$)•(cos$\frac{x}{2}$,-sin$\frac{x}{2}$)=cos$\frac{3x}{2}$cos$\frac{x}{2}$-sin$\frac{3x}{2}$sin$\frac{x}{2}$=cos($\frac{3x}{2}$+$\frac{x}{2}$)=cos2x,
当m=0时,f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$+1=cos2x+1,
则f($\frac{π}{6}$)=cos(2×$\frac{π}{6}$)+1=cos$\frac{π}{3}$+1=$\frac{1}{2}+1=\frac{3}{2}$;
(2)∵x∈[-$\frac{π}{3}$,$\frac{π}{4}$],
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{2+2cos2x}$=$\sqrt{4co{s}^{2}x}$=2cosx,
则f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-m|$\overrightarrow{a}$+$\overrightarrow{b}$|+1=cos2x-2mcosx+1=2cos2x-2mcosx,
令t=cosx,则$\frac{1}{2}$≤t≤1,
则y=2t2-2mt,对称轴t=$\frac{m}{2}$,
①当$\frac{m}{2}$<$\frac{1}{2}$,即m<1时,
当t=$\frac{1}{2}$时,函数取得最小值此时最小值y=$\frac{1}{2}$-m=-1,得m=$\frac{3}{2}$(舍),
②当$\frac{1}{2}$≤$\frac{m}{2}$≤1,即m<1时,
当t=$\frac{m}{2}$时,函数取得最小值此时最小值y=-$\frac{{m}^{2}}{2}$=-1,得m=$\sqrt{2}$,
③当$\frac{m}{2}$>1,即m>2时,
当t=1时,函数取得最小值此时最小值y=2-2m=-1,得m=$\frac{3}{2}$(舍),
综上若f(x)的最小值为-1,则实数m=$\sqrt{2}$.
(3)令g(x)=2cos2x-2mcosx+$\frac{24}{49}$m2=0,得cosx=$\frac{3m}{7}$或$\frac{4m}{7}$,
∴方程cosx=$\frac{3m}{7}$或$\frac{4m}{7}$在x∈[-$\frac{π}{3}$,$\frac{π}{4}$]上有四个不同的实根,
则$\left\{\begin{array}{l}{\frac{\sqrt{2}}{2}≤\frac{3m}{7}<1}\\{\frac{\sqrt{2}}{2}≤\frac{4m}{7}<1}\\{\frac{3m}{7}≠\frac{4m}{7}}\end{array}\right.$,得$\left\{\begin{array}{l}{\frac{7\sqrt{2}}{6}≤m<\frac{7}{3}}\\{\frac{7\sqrt{2}}{8}≤m<\frac{7}{4}}\\{m≠0}\end{array}\right.$,则$\frac{7\sqrt{2}}{6}$≤m<$\frac{7}{4}$,
即实数m的取值范围是$\frac{7\sqrt{2}}{6}$≤m<$\frac{7}{4}$.
点评 本题主要考三角函数的性质,函数的零点以及复合函数的应用,综合性较强,运算量较大,有一定的难度.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
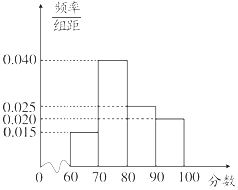 2016年年底,某商业集团根据相关评分标准,对所属20家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A,B,C,D四个类型,其考核评估标准如表:
2016年年底,某商业集团根据相关评分标准,对所属20家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A,B,C,D四个类型,其考核评估标准如表:| 评估得分 | [60,70) | [70,80) | [80,90) | [90,100] |
| 评分类型 | D | C | B | A |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
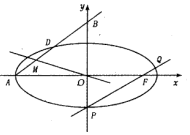 已知P(0,-1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足$\overrightarrow{PF}=7\overrightarrow{FQ}$.
已知P(0,-1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足$\overrightarrow{PF}=7\overrightarrow{FQ}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com