下图为某三角函数图象的一段, 正弦函数的解析式为y＝3sin( x- |
π |
![]() |
6 |
答案：T;T 解析：
|
解:(1)该函数的周期T= |
13π |
 |
3 |
|
- |
π |
|
3 |
|
＝4π, |
∴ω＝ |
2π |
|
T |
|
＝ ,又A＝3, 所给图象是曲线y＝3sin |
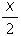沿x轴向右平移 |
π |
|
3 |
|
而得到的, 故所求函数解析式是 |
y＝3sin(x- |
π |
|
3 |
|
) |
＝3sin(x- |
π |
|
6 |
|
) |
(2)设(x,y)为y＝3sin(x- |
π |
|
6 |
|
)上的任意一点, 该点关于直线x＝2π |
的对称点应为(4π-x,y)故与y＝3sin(x- |
π |
|
6 |
|
) |
关于直线x＝2π对称的函数解析式是
y＝3sin( |
4π-x |
|
2 |
|
- |
π |
|
6 |
|
)＝-3sin(+ |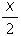
π |
|
6 |
|
) |
|
练习册系列答案
相关习题
|
