练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    甲，乙，丙三位学生独立地解同一道题，甲做对的概率为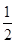，乙，丙做对的概率分别为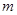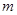， (＞)，且三位学生是否做对相互独立.记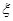为这三位学生中做对该题的人数，其分布列为：

    0

    1

    2

    3

    (Ⅰ)求至少有一位学生做对该题的概率；

    (Ⅱ)求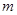，的值；

    (Ⅲ)求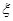的数学期望.

     

    【答案】

    (Ⅰ) ；（Ⅱ）；(Ⅲ) .

    【解析】

    试题分析：(Ⅰ) 至少有一位学生做对该题,它的对立事件是一个也没做对,故可利用对立事件来求；（Ⅱ）根据与列方程求出的值；(Ⅲ)由 的值，可求出，的值，从而求出的数学期望.

    试题解析：设“甲做对”为事件，“乙做对”为事件，“丙做对”为事件，由题意知，. 

    (Ⅰ)由于事件“至少有一位学生做对该题”与事件“”是对立的，所以至少有一位学生做对该题的概率是；

    (Ⅱ)由题意知，，整理得 ，,由，解得；

    （Ⅲ）由题意知，

    ，

    所以的数学期望为. 

    考点：1、独立事件的概率, 2、随机变量的数学期望.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•广州一模）甲，乙，丙三位学生独立地解同一道题，甲做对的概率为
    1
    2
    ，乙，丙做对的概率分别为m，n（m＞n），且三位学生是否做对相互独立．记ξ为这三位学生中做对该题的人数，其分布列为：
    ξ 0 1 2 3
    P
    1
    4
    		 a b
    1
    24
    （1）求至少有一位学生做对该题的概率；
    （2）求m，n的值；
    （3）求ξ的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•绍兴一模）甲、乙、丙三位学生在学校开设的三门选修课中自主选课，其中甲和乙各选修其中的两门，丙选修其中的一门，且每门选修课这三位学生中至少有一位选修，则不同的选法共有
    21
    21
    种．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年广东省广州市高三3月毕业班综合测试（一）理科数学试卷（解析版） 题型：解答题

    （本小题满分12分）

    甲，乙，丙三位学生独立地解同一道题，甲做对的概率为，乙，丙做对的概率分别为， (＞)，且三位学生是否做对相互独立.记为这三位学生中做对该题的人数，其分布列为：

    0

    1

    2

    3

    （1) 求至少有一位学生做对该题的概率；

    （2) 求，的值；

    （3) 求的数学期望.

     

    查看答案和解析>>

    科目：高中数学 来源：2010年四川省高二下学期5月月考数学试题 题型：选择题

    甲、乙、丙三位学生用计算机联网学习数学，每天上课后独立完成6道自我检测题，甲答及格的概率为，乙答及格的概率为，丙答及格的概率为，三人各答一次，则三人中只有一人答及格的概率为（   ）

    A．    B．    C．    D．以上答案都不对

     

    查看答案和解析>>

    同步练习册答案