
| A. | $\frac{9}{8}$ | B. | 2-$\frac{\sqrt{3}}{2}$ | C. | $\frac{25}{16}$ | D. | $\sqrt{3}$-$\frac{1}{2}$ |
分析 画出函数f(x)=$\left\{\begin{array}{l}{|lnx|,0<x≤2}\\{f(4-x),2<x<4}\end{array}$的图象,结合对数函数的图象和性质,可得x1•x2=1,x1+x2>$2\sqrt{{x}_{1}{x}_{2}}$=2,(4-x3)•(4-x4)=1,且x1+x2+x3+x4=8,则不等式kx3x4+x12+x22≥k+11恒成立,可化为:k≥$\frac{11-({x}_{1}^{2}+{x}_{2}^{2})}{{x}_{3}•{x}_{4}-1}$恒成立,求出$\frac{11-({x}_{1}^{2}+{x}_{2}^{2})}{{x}_{3}•{x}_{4}-1}$的最大值,可得k的范围,进而得到实数k的最小值.
解答 解:函数f(x)=$\left\{\begin{array}{l}{|lnx|,0<x≤2}\\{f(4-x),2<x<4}\end{array}$的图象如下图所示: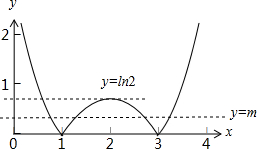
当方程f(x)=m有四个不等实根x1,x2,x3,x4(x1<x2<x3<x4)时,
|lnx1|=|lnx2|,即x1•x2=1,x1+x2>$2\sqrt{{x}_{1}{x}_{2}}$=2,
|ln(4-x3)|=|(4-x4)|,即(4-x3)•(4-x4)=1,
且x1+x2+x3+x4=8,
若不等式kx3x4+x12+x22≥k+11恒成立,
则k≥$\frac{11-({x}_{1}^{2}+{x}_{2}^{2})}{{x}_{3}•{x}_{4}-1}$恒成立,
由$\frac{11-({x}_{1}^{2}+{x}_{2}^{2})}{{x}_{3}•{x}_{4}-1}$=$\frac{11-{({x}_{1}^{\;}+{x}_{2}^{\;})}^{2}+2{x}_{1}{x}_{2}}{4({x}_{3}+{x}_{4})-16}$=$\frac{13-{({x}_{1}^{\;}+{x}_{2}^{\;})}^{2}}{16-4({x}_{1}+{x}_{2})}$=$\frac{1}{4}$[(x1+x2)-4$+\frac{3}{{(x}_{1}+{x}_{2})-4}$+8]≤2-$\frac{\sqrt{3}}{2}$
故k≥2-$\frac{\sqrt{3}}{2}$,
故实数k的最小值为2-$\frac{\sqrt{3}}{2}$,
故选:B
点评 本题考查的知识点是分段函数的应用,对数函数的图象和性质,函数的最值,函数恒成立问题,综合性强,转化困难,属于难题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
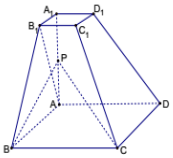 已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为AA1的中点.
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 16 | C. | 18 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com