
【题目】已知正方体ABCD-A1B1C1D1的棱长为2,E为棱CC1的中点,点M在正方形BCC1B1内运动,且直线AM//平面A1DE,则动点M 的轨迹长度为( )
A. ![]() B. π C. 2 D.
B. π C. 2 D. ![]()
【答案】D
【解析】
设平面DA1E与直线B1C1交于点F,连接AF、EF,则F为B1C1的中点.分别取B1B、BC的中点N、O,连接AN、ON、AO,可证出平面A1DE∥平面ANO,从而得到NO是平面BCC1B1内的直线.由此得到点M的轨迹被正方形BCC1B1截得的线段是线段ON.
解:设平面DA1E与直线B1C1交于点F,连接AF、EF,
则F为B1C1的中点.
分别取B1B、BC的中点N、O,连接AN、ON、AO,
则∵A1F∥AO,AN∥DE,A1F,DE平面A1DE,
AO,AN平面ANO,
∴A1F∥平面ANO.同理可得DE∥平面ANO,
∵A1F、DE是平面A1DE内的相交直线,
∴平面A1DE∥平面ANO,
所以NO∥平面A1DE,
∴直线NO平面A1DE,
∴M的轨迹被正方形BCC1B1截得的线段是线段NO.
∴M的轨迹被正方形BCC1B1截得的线段长NO![]() .
.
故选:D.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:
【题目】如图,将长为4,宽为1的长方形折叠成长方体ABCD-A1B1C1D1的四个侧面,记底面上一边![]() ,连接A1B,A1C,A1D.
,连接A1B,A1C,A1D.

(1)求长方体ABCD-A1B1C1D1体积的最大值 ;
(2)当长方体ABCD-A1B1C1D1的体积最大时,求二面角B-A1C-D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】基于移动互联技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,带给人们新的出行体验.某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司最近六个月内的市场占有率进行了统计,结果如下表:
月份 | 2017.8 | 2017.9 | 2017.10 | 2017.11 | 2017.12 | 2018.1 |
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
市场占有率 | 11 | 13 | 16 | 15 | 20 | 21 |
(1)请在给出的坐标纸中作出散点图,并用相关系数说明可用线性回归模型拟合月度市场占有率![]() 与月份代码
与月份代码![]() 之间的关系;
之间的关系;
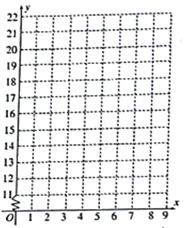
(2)求![]() 关于
关于![]() 的线性回归方程,并预测该公司2018年2月份的市场占有率;
的线性回归方程,并预测该公司2018年2月份的市场占有率;
(3)根据调研数据,公司决定再采购一批单车扩大市场,现有采购成本分别为1000元/辆和800元/辆的![]() 两款车型报废年限各不相同.考虑到公司的经济效益,该公司决定先对两款单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
两款车型报废年限各不相同.考虑到公司的经济效益,该公司决定先对两款单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
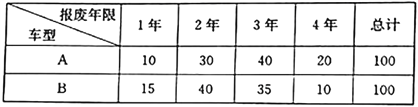
经测算,平均每辆单车每年可以为公司带来收入500元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且用频率估计每辆单车使用寿命的概率,以每辆单车产生利润的期望值为决策依据.如果你是该公司的负责人,你会选择采购哪款车型?
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
参考公式:相关系数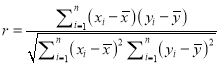 ;
;
回归直线方程为![]() ,其中
,其中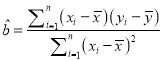 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学现有6名包含![]() 在内的男志愿者和4名包含
在内的男志愿者和4名包含![]() 在内的女志愿者,这10名志愿者要参加第十三届全运会支援服务工作,从这些人中随机抽取5人参加田赛服务工作,另外5人参加径赛服务工作.
在内的女志愿者,这10名志愿者要参加第十三届全运会支援服务工作,从这些人中随机抽取5人参加田赛服务工作,另外5人参加径赛服务工作.
(1)求参加田赛服务工作的志愿者中包含![]() 但不包含
但不包含![]() 的概率;
的概率;
(2)设![]() 表示参加径赛服务工作的女志愿者人数,求随机变量
表示参加径赛服务工作的女志愿者人数,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象过点
的图象过点![]() ,且不等式
,且不等式![]() 的解集为
的解集为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 在区间
在区间![]() 上有最小值
上有最小值![]() ,求实数
,求实数![]() 的值;
的值;
(3)设![]() ,若当
,若当![]() 时,函数
时,函数![]() 的图象恒在
的图象恒在![]() 图象的上方,求实数m的取值范围.
图象的上方,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
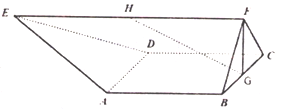
【题目】如图,在多面体![]() 中,已知
中,已知![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 为正三角形,
为正三角形, ![]() 分别为
分别为![]() 的中点,
的中点, ![]() 且
且![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(-2,0),B(2,0),曲线C上的动点P满足![]() .
.
(1)求曲线C的方程;
(2)若过定点M(0,-2)的直线l与曲线C有公共点,求直线l的斜率k的取值范围;
(3)若动点Q(x,y)在曲线C上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
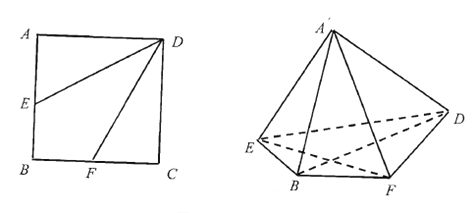
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,将
的中点,将![]() ,
, ![]() ,分别沿
,分别沿![]() ,
, ![]() 折起,使
折起,使![]() ,
, ![]() 两点重合于点
两点重合于点![]() ,连接
,连接![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com